Trả lời bởi giáo viên
Đáp án đúng: c
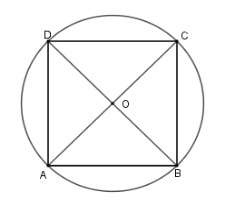
Gọi ABCD làhình vuông cạnh a nội tiếp đường tròn (O) suy ra O là giao điểm hai đường chéo AC và BD
Từ đó R=OA=AC2⇒AC=2R
Theo định lý Pytago ta có AB2+BC2=AC2⇒AC2=a2+a2⇔AC2=2a2
⇒AC=a√2=2R⇒a=√2R.
Hướng dẫn giải:
+ Sử dụng tính chất hình vuông để tìm bán kính đường tròn
+ Sử dụng định lý Pytago để tìm cạnh của hình vuông

