Câu hỏi:
3 năm trước
Cho lục giác đều \(ABCDEF\) cạnh \(a\) nội tiếp đường tròn tâm \(O\) . Tính bán kính đường tròn \(\left( O \right)\) theo \(a.\)
Trả lời bởi giáo viên
Đáp án đúng: c
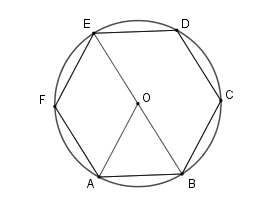
Ta có \(AB = BC = CD = DE = EF = FA\) nên số đo cung \(AB = \dfrac{1}{6}\) số đo cả đường tròn
Hay \(\widehat {AOB} = \dfrac{{360^\circ }}{6} = 60^\circ \) .
Suy ra tam giác \(AOB\) đều nên \(OA = OB = AB = a.\)
Vậy bán kính đường tròn \(\left( O \right)\) là \(a.\)
Hướng dẫn giải:
+ Sử dụng tính chất lục giác đều và tính chất tam giác đều

