Trả lời bởi giáo viên
Đáp án đúng: c
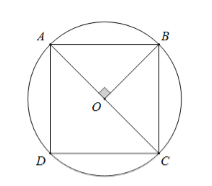
Hình vuông ABCD nội tiếp đường tròn \(\left( O \right) \Rightarrow O\) là tâm của hình vuông
Vì ABCD là hình vuông nên 2 đường chéo vuông góc với nhau, đồng thời chúng bằng nhau và cắt nhau tại trung điểm mỗi đường \( \Rightarrow OA \bot OB\) và OA = OB
\( \Rightarrow \Delta OAB\) vuông cân tại O
Gọi R là bán kính của đường tròn ngoại tiếp (O), ta có $AB = OA\sqrt 2 = R\sqrt 2 \Rightarrow R = \dfrac{{AB}}{{\sqrt 2 }} = \dfrac{2}{{\sqrt 2 }} = \sqrt 2 $
Hướng dẫn giải:
Nắm vững định nghĩa đường tròn ngoại tiếp và sử dụng định lý Pi-ta-go để tính cạnh huyền của tam giác vuông cân

