Câu hỏi:
3 năm trước
Tính cạnh của một ngũ giác đều ngoại tiếp đường tròn bán kính \(5\,cm\) (làm tròn đến chữ số thập phân thứ nhất).
Trả lời bởi giáo viên
Đáp án đúng: b
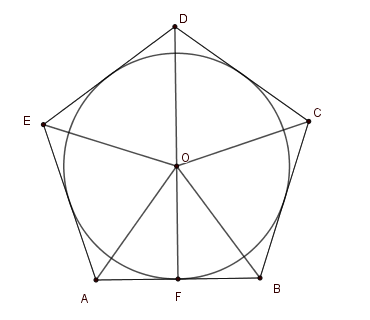
Gọi \(O\) là tâm đường tròn ngoại tiếp ngũ giác đều \(ABCDE\), đường cao \(OF \bot AB\) . Khi đó bán kính của \(\left( O \right)\) là \(OF = 5\,cm\) .
Ta có \(\widehat {AOB} = \dfrac{{360^\circ }}{5} = 72^\circ \)\( \Rightarrow \widehat {BOF} = 36^\circ \)
Xét tam giác \(OFB\) có \(FB = OF.\tan 36^\circ = 5.\tan 36^\circ \Rightarrow AB = 10.\tan 36^\circ \approx 7,3\) \(cm\) .
Hướng dẫn giải:
+ Sử dụng tính chất ngũ giác đều để tính góc \(AOB\)
+ Sử dụng hệ thức giữa cạnh và góc trong tam giác.

