Qua điểm \(A\) nằm ngoài đường tròn \(\left( O \right)\) kẻ hai cát tuyến \(ABC\) và \(ADE\) với đường tròn đó (\(B\) nằm giữa \(A\) và \(C,\)\(D\) nằm giữa \(A\) và \(E\)). Kẻ dây \(BF//DE.\) Khi đó kết luận đúng là:

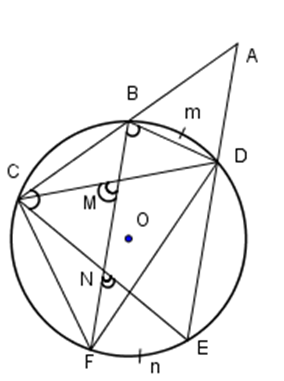
Ta có \(\widehat {BCD}\) là góc nội tiếp chắn cung \(BmD\,\,\left( 1 \right).\)

Ta có \(\widehat {FCE}\) là góc nội tiếp chắn cung \(FnE\,\,\left( 2 \right).\)

Mặt khác ta có \(sđ\overparen{BmD}\, = sđ\overparen{FnE}\,\,\left( 3 \right).\) (hai cung bị chắn bởi hai dây song song)

Từ \(\left( 1 \right),\,\left( 2 \right),\,\left( 3 \right)\) suy ra \(\widehat {FCE} = \widehat {BCD} \Rightarrow \widehat {FCE} + \widehat {ECD} = \widehat {BCD} + \widehat {ECD}.\)

Do đó \(\widehat {FCD} = \widehat {ECB}\,\left( 4 \right).\)

Theo tính chất về góc có đỉnh bên ngoài đường tròn ta có

\(\widehat {CAE} = \dfrac{1}{2}\left( {sđ\overparen{CFE} - sđ\overparen{BmD}} \right) = \dfrac{1}{2}\left( {sđ\,\overparen{CFE} - sđ\overparen{FnE}} \right) = \dfrac{1}{2}sđ\,\overparen{CF}\,\,\left( 5 \right).\)

Theo tính chất của góc nội tiếp bị chắn bởi cung ta có $\widehat {CDF} = \dfrac{1}{2}sđ\overparen{CF}\,\,\left( 6 \right).$

Từ \(\left( 5 \right)\) và \(\left( 6 \right)\) ta nhận được \(\widehat {CAE} = \widehat {CDF}\,\,\left( 7 \right).\)

Từ \(\left( 4 \right)\) và \(\left( 7 \right)\) ta nhận được \(\Delta ACE \backsim \Delta DCF\) (g-g)

Do đó \(\dfrac{{AC}}{{DC}} = \dfrac{{AE}}{{DF}} = \dfrac{{CE}}{{CF}} \Rightarrow AC.DF = AE.DC.\)