Câu hỏi:
2 năm trước
Một vật chịu tác dụng của $2$ lực song song cùng chiều có độ lớn lần lượt là $F_1 = 20N$ và $F_2$, hợp lực của chúng có độ lớn $F = 50N$ và giá của hợp lực \(\overrightarrow {\rm{F}} \) cách giá của \(\overrightarrow {{{\rm{F}}_1}} \) một đoạn $30cm$. Độ lớn của lực \(\overrightarrow {{{\rm{F}}_{\rm{2}}}} \) và khoảng cách từ giá hợp lực đến giá \(\overrightarrow {{{\rm{F}}_{\rm{2}}}} \) là:
Trả lời bởi giáo viên
Đáp án đúng: a
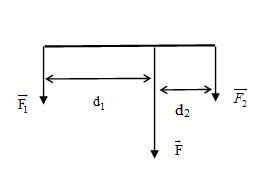
Áp dụng công thức tính độ lớn của hợp lực hai lực song song cùng chiều:
\(F = {F_1} + {F_2} < = > 50 = 20 + {F_2} < = > {F_2} = 30\,N\)
Gọi \({d_1}\) là khoảng cách từ giá của lực \(\overrightarrow {{F_1}} \)đến giá của hợp lực F, \({d_2}\) là khoảng cách từ giá của lực \(\overrightarrow {{F_2}} \) đến giá của hợp lực F. Ta có:
\(\frac{{{F_1}}}{{{F_2}}} = \frac{{{d_2}}}{{{d_1}}} < = > \frac{{{d_2}}}{{{d_1}}} = \frac{{20}}{{30}} = \frac{2}{3} < = > {d_2} = 20cm\)
Vậy độ lớn của lực \(\overrightarrow {{{\rm{F}}_{\rm{2}}}} \) là 30 N và khoảng cách từ giá hợp lực đến giá \(\overrightarrow {{{\rm{F}}_{\rm{2}}}} \) là 20cm
Hướng dẫn giải:
Áp dụng biểu thức quy tắc hợp hai lực song song cùng chiều : \(F = {F_1} + {F_2}\) và \(\frac{{{F_1}}}{{{F_2}}} = \frac{{{d_2}}}{{{d_1}}}\)
Trong đó:
+ \({d_1}\) là khoảng cách từ giá của lực \(\overrightarrow {{F_1}} \) đến giá của hợp lực \(\overrightarrow F \)
+ \({d_2}\) là khoảng cách từ giá của lực \(\overrightarrow {{F_2}} \) đến giá của hợp lực \(\overrightarrow F \)
Câu hỏi khác
- Bài tập momen của lực - điều kiện cân bằng của một vật rắn có trục quay cố định lý 10 có lời giải
- Bài tập quy tắc hợp hai lực song song cùng chiều lý 10 có lời giải
- Bài tập vật rắn lý 10 có lời giải
- Bài tập quy tắc hợp lực đồng quy lý 10 có lời giải
- Bài tập trắc nghiệm cân bằng tổng quát của vật rắn
