Câu hỏi:
2 năm trước
Một lực song song cùng chiều, có độ lớn \({F_1} = 5N,{F_2} = 15N\) đặt tại hai đầu một thanh nhẹ (khối lượng không đáng kể). AB dài \(20cm\). Hợp lực \(\overrightarrow F = \overrightarrow {{F_1}} + \overrightarrow {{F_2}} \) đặt cách đầu A bao nhiêu và có độ lớn bằng bao nhiêu?
Trả lời bởi giáo viên
Đáp án đúng: a
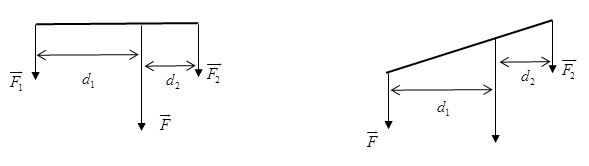
Để tính độ lớn hợp lực của hai lực song song cùng chiều ta áp dụng:
\(F = {F_1} + {F_2} = 5 + 15 = 20\,N\)
Gọi \({d_1}\) là khoảng cách từ giá của lực \({F_1}\) đến giá của hợp lực F, \({d_2}\) là khoảng cách từ giá của lực \({F_2}\) đến giá của hợp lực F. Ta có:
\(\dfrac{{{F_1}}}{{{F_2}}} = \dfrac{{{d_2}}}{{{d_1}}} = > \dfrac{{{d_2}}}{{{d_1}}} = \dfrac{1}{3}\)(1) và \({d_1} + {d_2} = 20\) vì giá của hai lực thành phần cách nhau 20cm (2)
Từ (1) và (2) ta có: \({d_1} = 15cm,\,{d_2} = 5cm\)
Vậy độ lớn của hợp lực là 20N và khoảng cách từ giá hợp lực đến giá của \(\overrightarrow {{{\rm{F}}_1}} \) là 15cm
Hướng dẫn giải:
Áp dụng biểu thức quy tắc hợp hai lực song song cùng chiều : \(F = {F_1} + {F_2}\) và \(\dfrac{{{F_1}}}{{{F_2}}} = \dfrac{{{d_2}}}{{{d_1}}}\)
Trong đó: \({d_1}\) là khoảng cách từ giá của lực \(\overrightarrow {{F_1}} \) đến giá của hợp lực \(\overrightarrow F \)
\({d_2}\) là khoảng cách từ giá của lực \(\overrightarrow {{F_2}} \) đến giá của hợp lực \(\overrightarrow F \)
Câu hỏi khác
- Bài tập momen của lực - điều kiện cân bằng của một vật rắn có trục quay cố định lý 10 có lời giải
- Bài tập quy tắc hợp hai lực song song cùng chiều lý 10 có lời giải
- Bài tập vật rắn lý 10 có lời giải
- Bài tập trắc nghiệm cân bằng tổng quát của vật rắn
- Bài tập quy tắc hợp lực đồng quy lý 10 có lời giải
