Câu hỏi:
2 năm trước
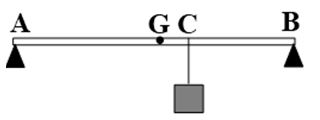
Một thanh AB dài \(1m\) khối lượng \(5kg\) được đặt nằm ngang lên hai giá đỡ tại A và B. Người ta móc vào điểm C của thanh \(\left( {AC = 60cm} \right)\) một vật có khối lượng \(10kg\). Lực nén lên hai giá đỡ là \(\left( {g = 10m/{s^2}} \right)\)
Trả lời bởi giáo viên
Đáp án đúng: b
Phân tích các lực tác dụng lên thanh như hình.
Ta có: \({F_1} + {F_2} = {P_1} + {P_2} = 150\) (1)
Gọi \({d_1},{d_2}\) là khoảng cách từ các lực \(\overrightarrow {{P_1}} ,\overrightarrow {{P_2}} \) tới vị trí trọng tâm mới của vật:
Ta có: \({d_1} + {d_2} = 10cm\) (2)
Lại có: \(\dfrac{{{d_2}}}{{{d_1}}} = \dfrac{{{P_1}}}{{{P_2}}} = \dfrac{1}{2} \Rightarrow {d_1} = 2{d_2}\) (3)
Từ (2) và (3) ta suy ra: \(\left\{ \begin{array}{l}{d_1} = \dfrac{{20}}{3}cm\\{d_2} = \dfrac{{10}}{3}cm\end{array} \right.\)
\( \Rightarrow \) Khoảng cách từ các lực \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} \) đến trọng tâm mới của vật là \(\left\{ \begin{array}{l}OA = 50 + \dfrac{{20}}{3} = \dfrac{{170}}{3}cm\\OB = 100 - OA = \dfrac{{130}}{3}cm\end{array} \right.\)
\( \Rightarrow \dfrac{{{F_1}}}{{{F_2}}} = \dfrac{{OB}}{{OA}} = \dfrac{{\dfrac{{130}}{3}}}{{\dfrac{{170}}{3}}} = \dfrac{{13}}{{17}}\)
\( \Rightarrow 17{F_1} = 13{F_2}\) (4)
Từ (1) và (4) ta suy ra: \(\left\{ \begin{array}{l}{F_1} = 65N\\{F_2} = 85N\end{array} \right.\)
Hướng dẫn giải:
Áp dụng biểu thức quy tắc hợp hai lực song song cùng chiều : \(F = {F_1} + {F_2}\) và \(\dfrac{{{F_1}}}{{{F_2}}} = \dfrac{{{d_2}}}{{{d_1}}}\)
Trong đó: \({d_1}\) là khoảng cách từ giá của lực \(\overrightarrow {{F_1}} \) đến giá của hợp lực \(\overrightarrow F \)
\({d_2}\) là khoảng cách từ giá của lực \(\overrightarrow {{F_2}} \) đến giá của hợp lực \(\overrightarrow F \)
Câu hỏi khác
- Bài tập momen của lực - điều kiện cân bằng của một vật rắn có trục quay cố định lý 10 có lời giải
- Bài tập quy tắc hợp hai lực song song cùng chiều lý 10 có lời giải
- Bài tập vật rắn lý 10 có lời giải
- Bài tập quy tắc hợp lực đồng quy lý 10 có lời giải
- Bài tập trắc nghiệm cân bằng tổng quát của vật rắn
