Câu hỏi:
2 năm trước
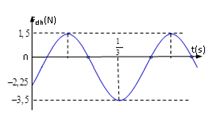
Một con lắc lò xo treo thẳng đứng có độ cứng \(k = 25N/m\) dao động điều hòa theo phương thẳng đứng. Biết trục Ox thẳng đứng hướng xuống, gốc $O$ trùng với $VTCB$. Biết giá trị đại số của lực đàn hồi tác dụng lên vật biến thiên theo đồ thị. Phương trình dao động của vật là
Trả lời bởi giáo viên
Đáp án đúng: c
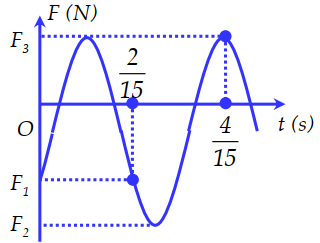
Từ đồ thị ta có hệ:
\(\begin{array}{l}\left\{ \begin{array}{l}k(A - \Delta {l_0}) = 1,5\\k(A + \Delta {l_0}) = 3,5\end{array} \right.\\ \Rightarrow A = \dfrac{5}{2}\Delta {l_0}\\ \Rightarrow \left\{ \begin{array}{l}\Delta {l_0} = 0,04m = 4cm\\A = 0,1m = 10cm\end{array} \right.\\ \Rightarrow \omega = \sqrt {\dfrac{g}{{\Delta {l_0}}}} = 5\sqrt {10} \approx 5\pi (rad/s)\end{array}\)
Biểu thức của lực đàn hồi có dạng: \(F = - k(\Delta {l_0} + x) = - 1 - 2,5\cos (5\pi t + \varphi )N\)
Lúc \(t = 0,{\rm{ }}F = - 2,25cos\varphi = - 1,25 \Rightarrow cos\varphi = \dfrac{1}{2} \Rightarrow \varphi = \dfrac{\pi }{3}\)
Vậy phương trình dao động của vật là: \(x = 10\cos \left( {5\pi t + \dfrac{\pi }{3}} \right)cm\)
Hướng dẫn giải:
+ Đọc đồ thị $F – t$
+ Sử dụng biểu thức tính lực đàn hồi cực đại, cực tiểu:
- Lực đàn hồi cực đại: \({F_{d{h_{{\rm{max}}}}}} = k\left( {A + \Delta {l_0}} \right)\)
- Lực đàn hồi cực tiểu: \({F_{d{h_{\min }}}} = k\left( {A - \Delta {l_0}} \right)\)
+ Biểu thức của lực đàn hồi: \({F_{dh}} = - k\left( {\Delta {l_0} + x} \right)\)
+ Xác định thời điểm ban đầu \(t = 0\) thì \(F = ?\)
Câu hỏi khác
- Bài tập lí thuyết dao động điều hòa có lời giải MÔN LÝ lớp 12
- Bài tập xác định thời gian vật chuyển động từ x1 đến x2, số lần qua li độ x có lời giải MÔN LÝ lớp 12
- Bài tập các đại lượng đặc trưng của DĐĐH có lời giải MÔN LÝ lớp 12
- Bài tập xác định quãng đường, tốc độ trung bình của vật trong DĐĐH có lời giải MÔN LÝ lớp 12
- Bài tập viết phương trình dao động điều hòa có lời giải MÔN LÝ lớp 12
