Một con lắc lò xo nằm ngang, dao động điều hòa có đồ thị li độ theo thời gian như hình vẽ.
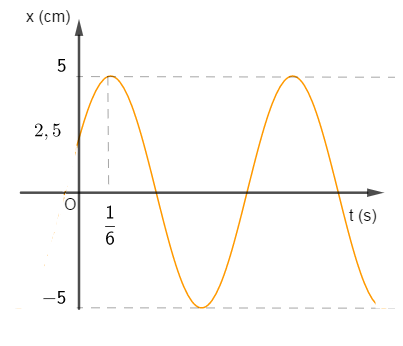
Kể từ thời điểm ban đầu \(t = 0\), lực đàn hồi đổi chiều lần đầu tại thời điểm
Trả lời bởi giáo viên
+ Từ đồ thị dao động, ta có:
- Biên độ dao động: \(A = 5cm\)
- Thời gian đi từ \(\dfrac{A}{2} \to A\): \(\Delta t = \dfrac{T}{6} = \dfrac{1}{6}s \to T = 1s\)
+ Tại thời điểm ban đầu, vật đang đang ở li độ \(x = \dfrac{A}{2}\) và chuyển động theo chiều dương
+ Lực đàn hồi của con lắc lò xo nằm ngang đổi chiều tại vị trí cân bằng
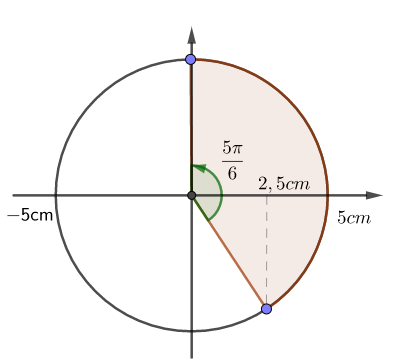
Từ vòng tròn lượng giác,
=> Lực đàn hồi đổi chiều lần đầu kể từ t = 0 tại thời điểm: \(\Delta t = \dfrac{{\Delta \varphi }}{\omega } = \dfrac{{\dfrac{{5\pi }}{6}}}{{\dfrac{{2\pi }}{T}}} = \dfrac{{5T}}{{12}} = \dfrac{5}{{12}}s\)
Hướng dẫn giải:
+ Đọc đồ thi x – t, xác định các đại lượng:
- Biên độ
- Chu kì
- Vị trí tại thời điểm ban đầu
+ Xác định vị trí lực đàn hồi đổi chiều
+ Sử dụng vòng tròn lượng giác và trục thời gian suy ra từ vòng tròn

