Một con lắc đơn có chu kì dao động T = 2 s. Nếu treo con lắc vào trần một toa xe đang chuyển động nhanh dần đều trên mặt đường nằm ngang thì thấy rằng ở vị trí cân bằng mới, dây treo con lắc hợp với phương thẳng đứng một góc α = 300. Cho g = 10 m/s2. Tìm chu kì dao động mới của con lắc trong toa xe và gia tốc của toa xe ?
Trả lời bởi giáo viên
Ta có:
+ Chu kì dao động của con lắc khi xe đứng yên: \(T = 2\pi \sqrt {\frac{l}{g}} = 2{\rm{s}}\)
Ta có, xe chạy trên đường ngang => Fqt vuông góc với trọng lực P
+ Chu kì dao động của con lắc khi xe chạy nhanh dần đều trên phương ngang: \(T' = 2\pi \sqrt {\frac{l}{{g'}}} \)
\(\begin{array}{l}\tan 30 = \frac{{{F_{qt}}}}{P} = \frac{a}{g} = \frac{1}{{\sqrt 3 }} \to a = \frac{g}{{\sqrt 3 }} = 5,77m/{s^2}\\g' = \sqrt {{g^2} + {a^2}} = \sqrt {{g^2} + \frac{{{g^2}}}{3}} = \frac{{2g}}{{\sqrt 3 }}\\ \to \frac{{T'}}{T} = \sqrt {\frac{g}{{g'}}} = \sqrt {\frac{g}{{\frac{{2g}}{{\sqrt 3 }}}}} = \sqrt {\frac{{\sqrt 3 }}{2}} = 0,93 \to T' = 0,93T = 1,86s\end{array}\)
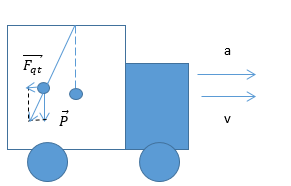
Hướng dẫn giải:
+ Áp dụng công thức tính chu kì dao động của con lắc đơn: \(T = 2\pi \sqrt {\frac{l}{g}} \)
+ Áp dụng bài toán con lắc đơn chịu thêm tác dụng của lực quán tính

