Một con lắc đơn chiều dài l và gắn vào vật có khối lượng m dao động điều hòa trên trục Ox với biên độ 10cm, chu kỳ 2s. Mốc thế năng ở vị trí cân bằng. Tốc độ trung bình của vật trong khoảng thời gian ngắn nhất khi chất điểm đi từ vị trí có động năng bằng 3 lần thế năng đến vị trí có động năng bằng 1/3 thế năng là:
Trả lời bởi giáo viên
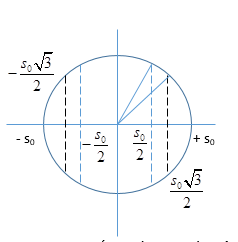
Tại vị trí 1: ${W_{{d_1}}} = 3{W_{{t_1}}} \to {s_1} = \pm \frac{{{s_0}}}{2}$
Tại vị trí 2:
${W_{{d_2}}} = \frac{1}{3}{W_{{t_2}}} \to {s_2} = \pm \frac{{{s_0}\sqrt 3 }}{2}$
=> Thời gian ngắn nhất khi chất điểm đi từ vị trí có động năng bằng 3 lần thế năng đến vị trí có động năng bằng 1/3 thế năng là: \({t_{\frac{{{s_0}}}{2} \to \frac{{{s_0}\sqrt 3 }}{2}}} = \frac{T}{{12}} = \frac{1}{6}s\)
Quãng đường vật đi được trong khoảng thời gian đó: \(S = \frac{{{s_0}\sqrt 3 }}{2} - \frac{{{s_0}}}{2} = 3,66cm\)
=> Tốc độ trung bình của vật: \({v_{tb}} = \frac{S}{t} = \frac{{3,66}}{{\frac{1}{6}}} = 21,96cm/s\)
Hướng dẫn giải:
+ Sử dụng biểu thức Wđ = nWt:
\(\left\{ \begin{array}{l}s = \pm \frac{{{s_0}}}{{\sqrt {n + 1} }}\\\alpha = \pm \frac{{{\alpha _0}}}{{\sqrt {n + 1} }}\end{array} \right.\)
+ Sử dụng vòng tròn lượng giác
+ Áp dụng công thức tính tốc độ trung bình: \({v_{tb}} = \frac{S}{t}\)

