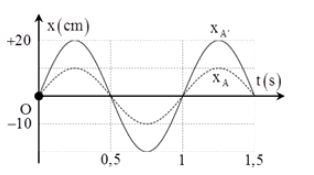
Điểm sáng $A$ đặt trên trục chính của một thấu kính, cách thấu kính \(30{\rm{ }}cm\), Chọn trục tọa độ $Ox$ vuông góc với trục chính của thấu kính, gốc $O$ nằm trên trục chính của thấu kính. Cho $A$ dao động điều hòa quanh vị trí cân bằng $O$ theo phương của trục $Ox$. Biết phương trình dao động của $A$ và ảnh $A'$ của nó qua thấu kính có đồ thị được biểu diễn như hình vẽ bên. Khoảng cách lớn nhất giữa vật sáng và ảnh của nó khi điểm sáng $A$ dao động có giá trị gần với
Trả lời bởi giáo viên
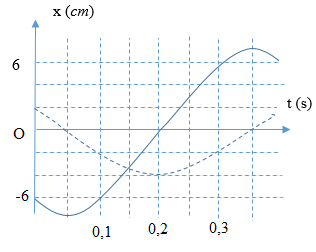
+ Từ đồ thị ta thấy vật $A$ và ảnh $A’$ dao động cùng pha nhau, $A’$ luôn gấp đôi vật $A$ \( \to \) thấu kính hội tụ cho ảnh ảo.
\( \to \) Công thức thấu kính: \(k = - \dfrac{{d'}}{d} = 2 \Rightarrow d' = 2{\rm{d}} = - 60\,\,cm.\)
+ Khoảng cách theo phương trục của thấu kính: \({\rm{d}} = 60 - 30 = 30\,\,cm.\)
+ Hai dao động cùng pha \( \to \Delta {x_{\max }} = \Delta A = 20 - 10 = 10\,\,cm.\)
\( \to \) Khoảng cách giữa $AA’$ là: \({\rm{AA}}' = \sqrt {{d^2} + \Delta x_{\max }^2} = 31,6\,\,cm.\)
Hướng dẫn giải:
Áp dụng công thức tính độ phóng đại của thấu kính \(k = - \dfrac{{d'}}{d}.\)