Câu hỏi:
2 năm trước
Đề thi THPT QG 2020 – mã đề 104
Cho hình lăng trụ đứng \(ABC.A'B'C'\) có tất cả các cạnh bằng \(a.\) Gọi \(M\) là trung điểm của \(AA'\) (tham khảo hình vẽ).
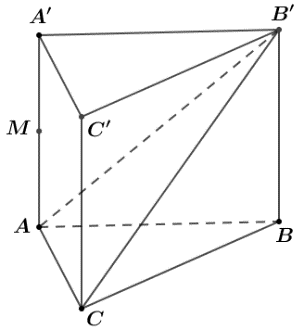
Khoảng cách từ \(M\) đến mặt phẳng \(\left( {AB'C} \right)\) bằng
Trả lời bởi giáo viên
Đáp án đúng: d
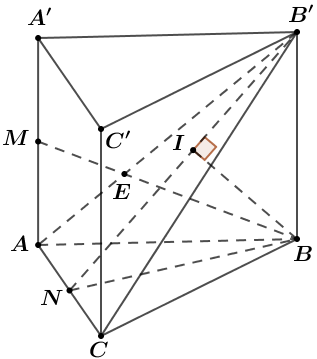
Trong \(\left( {ABB'A'} \right)\), gọi \(E\) là giao điểm của \(BM\) và \(AB'\).
Khi đó hai tam giác \(EAM\) và \(EB'B\) đồng dạng.
\( \Rightarrow \dfrac{{d\left( {M,\left( {AB'C} \right)} \right)}}{{d\left( {B,\left( {AB'C} \right)} \right)}} = \dfrac{{EM}}{{EB}} = \dfrac{{MA}}{{BB'}} = \dfrac{1}{2}\)\( \Rightarrow d\left( {M,\left( {AB'C} \right)} \right) = \dfrac{1}{2} \cdot d\left( {B,\left( {AB'C} \right)} \right)\).
Từ \(B\) kẻ \(BN \bot AC\) thì \(N\) là trung điểm của \(AC\) và \(BN = \dfrac{{a\sqrt 3 }}{2}\), \(BB' = a\).
Kẻ \(BI \bot B'N\) thì \(d\left( {B,\left( {AB'C} \right)} \right) = BI\)\( = \dfrac{{BB'.BN}}{{\sqrt {B{{B'}^2} + B{N^2}} }} = \dfrac{{a\sqrt {21} }}{7}\).
Vậy \(d\left( {M,\left( {AB'C} \right)} \right) = \dfrac{1}{2} \cdot d\left( {B,\left( {AB'C} \right)} \right) = \dfrac{{a\sqrt {21} }}{{14}}\).
Hướng dẫn giải:
Sử dụng phương pháp đổi điểm để tính \(d\left( {M;\,\,\left( {A'BC} \right)} \right).\)
