Đề thi THPT QG 2020 – mã đề 104
Cho hình chóp \(S.ABC\)có đáy \(ABC\) là tam giác vuông tại \(B\), \(AB = a\); \(BC = a\sqrt 2 \); \(SA\) vuông góc với mặt phẳng đáy và \(SA = a\). Góc giữa đường thẳng \(SC\) và đáy bằng
Trả lời bởi giáo viên
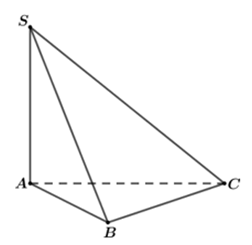
Ta có:\(SA \bot \left( {ABC} \right)\) \( \Rightarrow AC\) là hình chiếu của \(SC\) trên \(\left( {ABC} \right)\)
\( \Rightarrow \angle \left( {SC,\,\,\left( {ABC} \right)} \right) = \angle \left( {SC,\,\,AC} \right) = \angle SCA.\)
Áp dụng định lý Pitago cho \(\Delta SCA\) vuông tại \(A\) ta có: \(AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{a^2} + 2{a^2}} = a\sqrt 3 .\)
\( \Rightarrow \tan \angle SCA = \dfrac{{SA}}{{AC}} = \dfrac{a}{{a\sqrt 3 }} = \dfrac{1}{{\sqrt 3 }}\) \( \Rightarrow \angle SCA = {30^0}.\)
Hướng dẫn giải:
Góc giữa đường thẳng \(d\) và mặt phẳng \(\left( \alpha \right)\) là góc giữa đường thẳng \(d\) và đường thẳng \(d'\) với \(d'\) là hình chiếu của \(d\) trên \(\left( \alpha \right).\)