Đề thi THPT QG 2020 – mã đề 104

Cho hình chóp \(S.ABC\) có đáy là tam giác đều cạnh \(2a\), \(SA\) vuông góc với mặt phẳng đáy, góc giữa mặt phẳng \(\left( {SBC} \right)\) và mặt phẳng đáy bằng \({30^0}\). Diện tích của mặt cầu ngoại tiếp hình chóp \(S.ABC\) bằng

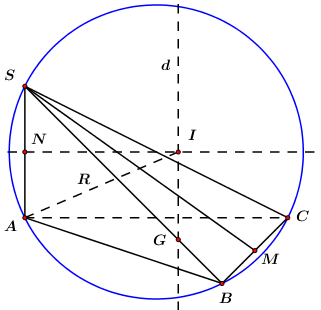
Gọi \(G\) là trọng tâm \(\Delta ABC\)

Ta có: \(SA \bot \left( {ABC} \right)\)

Qua \(G,\) dựng đường thẳng \(d\) song song với \(SA\) \( \Rightarrow d \bot \left( {ABC} \right)\)

Dựng đường trung trực của \(SA,\) cắt \(d\) tại \(I\) \( \Rightarrow I\) là tâm mặt cầu ngoại tiếp khối \(SABC.\)

\( \Rightarrow R = AI.\)

Gọi \(M,\,\,N\) lần lượt là trung điểm của \(BC\) và \(SA.\)

Ta có: \(\Delta ABC\) đều \( \Rightarrow AM \bot BC\) (tính chất tam giác đều).

Lại có: \(\Delta SBC\) cân tại \(S\) \( \Rightarrow SM \bot BC = \left\{ M \right\}\) (tính chất tam giác cân)

\( \Rightarrow \angle \left( {\left( {SBC} \right),\,\,\left( {ABC} \right)} \right) = \angle \left( {SM,\,\,AM} \right) = \angle SMA = {30^0}\)

\( \Rightarrow SA = AM.\tan {30^0} = \dfrac{{2a\sqrt 3 }}{2}.\dfrac{{\sqrt 3 }}{3} = a.\)

Có \(AG = \dfrac{2}{3}AM = \dfrac{2}{3}.\dfrac{{2a\sqrt 3 }}{2} = \dfrac{{2a\sqrt 3 }}{3}.\)

Ta có: \(ANIG\) là hình chữ nhật \( \Rightarrow AN = IG = \dfrac{1}{2}SA = \dfrac{a}{2}.\)

Áp dụng định lý Pitago cho \(\Delta AIG\) vuông tại \(G\) ta có:

\(R = AI = \sqrt {A{G^2} + G{I^2}} \) \( = \sqrt {{{\left( {\dfrac{a}{2}} \right)}^2} + {{\left( {\dfrac{{2a\sqrt 3 }}{3}} \right)}^2}}  = \dfrac{{a\sqrt {57} }}{6}.\)

\( \Rightarrow \) Diện tích mặt cầu ngoại tiếp hình chóp \(SABC\) là: \(S = 4\pi {R^2} = 4\pi .{\left( {\dfrac{{a\sqrt {57} }}{6}} \right)^2} = \dfrac{{19\pi {a^2}}}{3}.\)