Câu hỏi:
2 năm trước
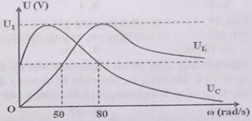
Đặt điện áp \(u = 200c{\rm{os}}\omega {\rm{t}}\left( V \right)\) (ω thay đổi được) vào hai đầu đoạn mạch mắc nối tiếp gồm cuộn cảm thuần có độ tự cảm L, điện trở R và tụ điện có điện dung C, với CR2<2L. Điện áp hiệu dụng giữa hai bản tụ điện và điện áp hiệu dụng hai đầu cuộn cảm lần lượt là UC , UL phụ thuộc vào ω, chúng được biểu diễn bằng các đồ thị như hình vẽ bên, tương ứng với các đường UC, UL. Giá trị của UM trong đồ thị gần nhất với giá trị nào sau đây?
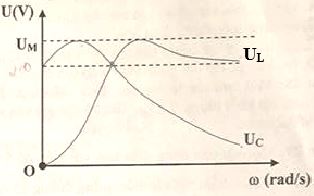
Trả lời bởi giáo viên
Đáp án đúng: b
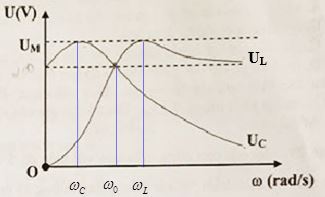
Gọi \({\omega _0}\) - là giá trị của \(\omega \) sao cho \({U_L} = {U_C}\)
\({\omega _C}\) - là giá trị của \(\omega \) sao cho \({U_{{C_{max}}}}\)
\({\omega _L}\) - là giá trị của \(\omega \) sao cho \({U_{{L_{max}}}}\)
+ Từ đồ thị, ta có:
\(\omega = 0\) và \(\omega = {\omega _0}\) đều cho \({U_C}\) như nhau
(Áp dụng bài toán \(\omega \) biến thiên có hai giá trị của \(\omega \) cho cùng hiệu điện thế \({U_C}\))
Khi đó ta có:
\(\omega _1^2 + \omega _2^2 = 2\omega _C^2 \Leftrightarrow {0^2} + \omega _0^2 = 2\omega _C^2\)
\( \Rightarrow {\omega _C} = \dfrac{{{\omega _0}}}{{\sqrt 2 }}\) (1)
+ Tại vị trí \(\omega = 0\), \({U_C} \approx U\)
+ Tại vị trí: \(\omega = {\omega _0}\), ta có \({U_C} = {U_R} = {U_L}\)
Nên ta suy ra: \({Z_{0C}} = R = {Z_{0L}}\) (2)
+ Tại vị trí: \(\omega = {\omega _C}\)
\(\begin{array}{l}{U_C} = {U_{{C_{max}}}} = \dfrac{{U{Z_C}}}{Z} = \dfrac{{U{Z_C}}}{{\sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }}\\ = \dfrac{{U\sqrt 2 {Z_{0C}}}}{{\sqrt {{R^2} + {{\left( {\dfrac{1}{{\sqrt 2 }}{Z_{0L}} - \sqrt 2 {Z_{0C}}} \right)}^2}} }} = \dfrac{{U\sqrt 2 R}}{{\sqrt {{R^2} + {{\left( {\dfrac{1}{{\sqrt 2 }}R - \sqrt 2 R} \right)}^2}} }}\\ = \dfrac{{U\sqrt 2 }}{{\sqrt {1 + \dfrac{1}{2}} }} = \dfrac{{U2\sqrt 3 }}{3}\end{array}\)
Theo đầu bài, ta có \(U = \dfrac{{200}}{{\sqrt 2 }} = 100\sqrt 2 V\)
\( \Rightarrow {U_M} = {U_{{C_{max}}}} = \dfrac{{100\sqrt 2 .2\sqrt 3 }}{3} = \dfrac{{200\sqrt 6 }}{3} \approx 163,3V\)
Hướng dẫn giải:
+ Phương pháp đọc đồ thị
+ \(\omega \) biến thiên có hai giá trị của \(\omega \) cho \({U_{{C_1}}} = {U_{{C_2}}}\): \(\omega _1^2 + \omega _2^2 = 2\omega _C^2\)
Câu hỏi khác
- Bài tập các mạch điện xoay chiều có lời giải MÔN LÝ lớp 12
- Bài tập mạch RLC mắc nối tiếp có lời giải MÔN LÝ lớp 12
- Bài tập pha u,i - viết phương trình u, i có lời giải MÔN LÝ lớp 12
- Bài tập lý thuyết đại cương về dòng điện xoay chiều có lời giải MÔN LÝ lớp 12
- Bài tập đại cương dòng điện xoay chiều có lời giải MÔN LÝ lớp 12
