Câu hỏi:
2 năm trước
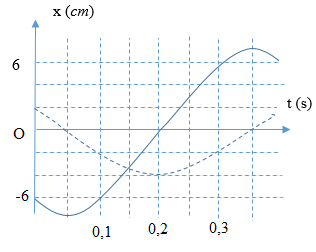
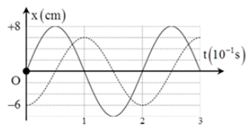
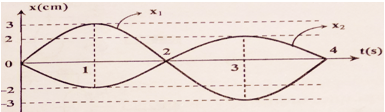
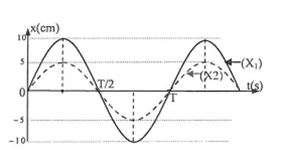
Có hai con lắc lò xo giống nhau đều có khối lượng vật nhỏ là \(m{\rm{ }} = {\rm{ }}400g\). Mốc thế năng tại vị trí cân bằng \({x_1},{\rm{ }}{x_2}\) lần lượt là đồ thị li độ theo thời gian của con lắc thứ nhất và thứ 2 như hình vẽ:
Tại thời điểm t con lắc thứ nhất có động năng \(0,06J\) và con lắc thứ hai có thế năng \(0,005J\). Chu kì của hai con lắc là:
Trả lời bởi giáo viên
Đáp án đúng: b
Từ đồ thị ta có phương trình dao động của từng vật là:\(\left\{ \begin{array}{l}{x_1} = 10\cos (\omega t - \frac{\pi }{2})\\{x_2} = 5\cos (\omega t - \frac{\pi }{2})\end{array} \right. \Rightarrow {x_2} = \frac{{{x_1}}}{2}\)
Xét tại thời điểm t ta có: \(\left\{ \begin{array}{l}{{\rm{W}}_{{\rm{d}}1}} = {\rm{W}} - {{\rm{W}}_{t1}} = \frac{1}{2}kA_1^2 - \frac{1}{2}kx_1^2 = 0,06J\,\,\,\,\,\left( 1 \right)\\{{\rm{W}}_{t2}} = \frac{1}{2}kx_2^2 = \frac{1}{2}k\frac{{x_1^2}}{4} = 0,005 \Leftrightarrow \frac{1}{2}kx_1^2 = 0,02\,\,\,\,\,\,\left( 2 \right)\end{array} \right.\)
Lấy (2) thế vào (1) ta có: \(\frac{1}{2}kA_1^2 = 0,06 + 0,02 = 0,08 \Leftrightarrow \frac{1}{2}k{.0,1^2} = 0,08 \Leftrightarrow k = 16\left( {N/m} \right)\)
Chu kì của 2 con lắc là: \(T = 2\pi .\sqrt {\frac{m}{k}} = 2\pi \sqrt {\frac{{0,4}}{{16}}} \approx 1s\)
Hướng dẫn giải:
- Sử dụng lí thuyết về phương trình dao động điều hòa
- Sử dụng các công thức trong dao động điều hòa của con lắc lò xo:
+ Cơ năng: \({\rm{W}} = {{\rm{W}}_d} + {{\rm{W}}_t} = \frac{1}{2}m{v^2} + \frac{1}{2}k{x^2} = \frac{1}{2}k{A^2}\)
+ Sử dụng công thức tính chu kì: \(T = 2\pi \sqrt {\frac{m}{k}} \)
Câu hỏi khác
- Bài tập lí thuyết dao động điều hòa có lời giải MÔN LÝ lớp 12
- Bài tập xác định thời gian vật chuyển động từ x1 đến x2, số lần qua li độ x có lời giải MÔN LÝ lớp 12
- Bài tập các đại lượng đặc trưng của DĐĐH có lời giải MÔN LÝ lớp 12
- Bài tập xác định quãng đường, tốc độ trung bình của vật trong DĐĐH có lời giải MÔN LÝ lớp 12
- Bài tập viết phương trình dao động điều hòa có lời giải MÔN LÝ lớp 12
