Câu hỏi:
2 năm trước
Có bao nhiêu số nguyên \(a \in \left( { - 2019;2019} \right)\) để phương trình \(\dfrac{1}{{\ln \left( {x + 5} \right)}} + \dfrac{1}{{{3^x} - 1}} = x + a\) có hai nghiệm phân biệt?
Trả lời bởi giáo viên
Đáp án đúng: d
\(\dfrac{1}{{\ln \left( {x + 5} \right)}} + \dfrac{1}{{{3^x} - 1}} = x + a \Leftrightarrow f\left( x \right) = \dfrac{1}{{\ln \left( {x + 5} \right)}} + \dfrac{1}{{{3^x} - 1}} - x = a\,\,\left( * \right)\).
Xét hàm số \(f\left( x \right) = \dfrac{1}{{\ln \left( {x + 5} \right)}} + \dfrac{1}{{{3^x} - 1}} - x\).
ĐKXĐ: \(\left\{ \begin{array}{l}x + 5 > 0\\\ln \left( {x + 5} \right) \ne 0\\{3^x} - 1 \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x > - 5\\x + 5 \ne 1\\{3^x} \ne 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x > - 5\\x \ne - 4\\x \ne 0\end{array} \right.\)
\( \Rightarrow D = \left( { - 5; - 4} \right) \cup \left( { - 4;0} \right) \cup \left( {0; + \infty } \right)\).
Ta có:
$f'\left( x \right) = - \frac{1}{{\left( {x + 5} \right){{\ln }^2}\left( {x + 5} \right)}} - \frac{{{3^x}\ln 3}}{{{{\left( {{3^x} - 1} \right)}^2}}} - 1 < 0,\forall x \in D$
BBT:
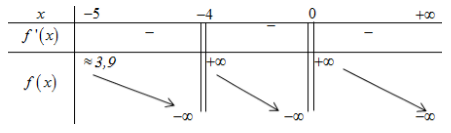
Từ BBT suy ra phương trình (*) có 2 nghiệm \( \Leftrightarrow a \ge 4\).
Kết hợp ĐK \( \Rightarrow a \in \left\{ {4;...;2018} \right\}\). Vậy có 2015 giá trị của \(a\) thỏa mãn.
Hướng dẫn giải:
+) Cô lập \(m\), đưa phương trình về dạng \(a = f\left( x \right)\).
+) Số nghiệm của phương trình \(a = f\left( x \right)\) là số giao điểm của đồ thị hàm số \(y = a\) và \(y = f\left( x \right)\).
+) Lập BBT hàm số \(y = f\left( x \right)\) và kết luận
