Câu hỏi:
2 năm trước
Cho tam giác nhọn \(ABC\;\left( {AB < AC} \right)\) nội tiếp đường tròn tâm \(O\), có ba đường cao là \(AD,BE,CF\) và trực tâm là \(H\). Gọi \(M\)là giao điểm của \(AO\) với \(BC\) và \(P,\;Q\)lần lượt là chân các đường vuông góc kẻ từ \(M\) đến \(AB,AC\).
Chọn đẳng thức đúng.
Trả lời bởi giáo viên
Đáp án đúng: a
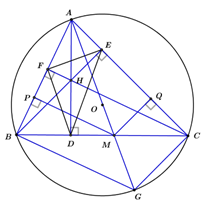
Ta có
\(\begin{array}{l}FH = AH.\sin \widehat {BAD} = AH.\dfrac{{BD}}{{AB}}\\PM = BM.\sin \widehat {ABD} = BM.\dfrac{{AD}}{{AB}}\\ \Rightarrow FH.PM = AH.BM.\dfrac{{BD}}{{AB}}.\dfrac{{AD}}{{AB}}.\end{array}\)\(\)
Chứng minh tương tự ta có:
\(HE.QM = AH.MC.\dfrac{{DC}}{{AC}}.\dfrac{{AD}}{{AC}}\)
Ta có : \(HE.MQ = HF.MP\)
\( \Rightarrow AH.BM.\dfrac{{BD}}{{AB}}.\dfrac{{AD}}{{AB}} = AH.MC.\dfrac{{DC}}{{AC}}.\dfrac{{AD}}{{AC}} \Rightarrow \dfrac{{BM}}{{MC}}.\dfrac{{BD}}{{DC}} = {\left( {\dfrac{{AB}}{{AC}}} \right)^2}\;.\)
Hướng dẫn giải:
Sử dụng biểu thức đã chứng minh ở câu trước \(MQ.HE = HF.MP\) , biến đổi để đưa về biểu thức cần tìm.
