Cho tam giác \(ABC\) vuông tại \(A\), \(BC = a\sqrt 3 \), \(M\) là trung điểm của \(BC\) và có \(\overrightarrow {AM} .\overrightarrow {BC} = \dfrac{{{a^2}}}{2}\). Tính cạnh \(AB\), \(AC\).
Trả lời bởi giáo viên
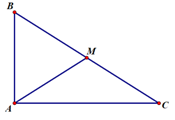
\(\overrightarrow {AM} \overrightarrow {BC} = \dfrac{{{a^2}}}{2}\) \( \Rightarrow \dfrac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right)\left( {\overrightarrow {AC} - \overrightarrow {AB} } \right) = \dfrac{{{a^2}}}{2}\) \( \Rightarrow A{C^2} - A{B^2} = {a^2}\).
Mặt khác, tam giác \(ABC\) vuông tại \(A\) nên \(A{B^2} + A{C^2} = 3{a^2}\).
Suy ra \(\left\{ \begin{array}{l}A{C^2} = 2{a^2}\\A{B^2} = {a^2}\end{array} \right.\) \( \Rightarrow \left\{ \begin{array}{l}AC = a\sqrt 2 \\AB = a\end{array} \right.\).
Hướng dẫn giải:
Lập hệ phương trình ẩn \(AB,AC\) và giải hệ tìm độ dài hai cạnh.




