Câu hỏi:
2 năm trước
Cho đường tròn tâm \(O\) bán kính \(R\) và điểm \(M\) thỏa mãn \(MO = 3R\). Một đường kính \(AB\) thay đổi trên đường tròn. Giá trị nhỏ nhất của biểu thức \(S = MA + MB\).
Trả lời bởi giáo viên
Đáp án đúng: a
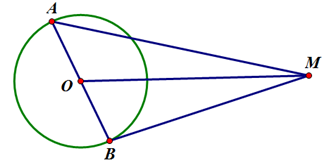
Gọi \(\widehat {MOA} = \alpha \Rightarrow \widehat {MOB} = 180^\circ - \alpha \).
Ta có \(MA = \sqrt {M{O^2} + A{O^2} - 2MO.AO.\cos \alpha } = \sqrt {9{R^2} + {R^2} - 6{R^2}\cos \alpha } = R\sqrt {10 - 6\cos \alpha } \).
\(MB = \sqrt {M{O^2} + B{O^2} - 2MO.BO.\cos \left( {180^\circ - \alpha } \right)} = \sqrt {9{R^2} + {R^2} + 6{R^2}\cos \alpha } = R\sqrt {10 + 6\cos \alpha } \).
Xét \(C = \sqrt {10 - 6\cos \alpha } + \sqrt {10 + 6\cos \alpha } \) \( \Rightarrow {C^2} = 20 + 2\sqrt {100 - 36{{\cos }^2}\alpha } \ge 20 + 2\sqrt {100 - 36} = 36\).
Suy ra \(C \ge 6\). Dấu xẩy ra khi ${\cos ^2}\alpha = 1 \Leftrightarrow \left[ \begin{array}{l}\cos \alpha = 1\\\cos \alpha = - 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\alpha = 0^\circ \\\alpha = 180^\circ \end{array} \right.$.
Ta có $S = MA + MB = R\left( {\sqrt {10 - 6\cos \alpha } + \sqrt {10 + 6\cos \alpha } } \right) \ge 6R$.
Suy ra \(\min S = 6R\) khi và chỉ khỉ \(A\), \(O\), \(B\), \(M\) thẳng hàng.
Hướng dẫn giải:
- Đặt \(\widehat {MOA} = \alpha \) và biểu diễn \(MA,MB\) theo \(\alpha \)
- Tìm GTNN của \(MA + MB\) theo \(\alpha \) và kết luận.
Câu hỏi khác
- Bài tập giá trị lượng giác của một góc bất kì từ 0 đến 180 độ toán 10 có lời giải
- Bài tập hệ thức lượng trong tam giác toán 10 có lời giải
- Bài tập tích vô hướng của hai véc tơ toán 10 có lời giải
- Bài tập biểu thức tọa độ của tích vô hướng toán 10 có lời giải
- Bài tập tổng hợp câu hay và khó chương tích vô hướng của hai véc tơ toán 10 có lời giải
