Câu hỏi:
2 năm trước
Cho tam giác đều ABC cạnh 18cm. Tập hợp các điểm M thỏa mãn đẳng thức |2→MA+3→MB+4→MC|=|→MA−→MB| là
Trả lời bởi giáo viên
Đáp án đúng: b
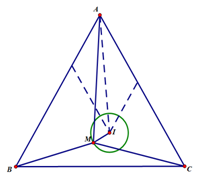
Ta có |→MA−→MB|=|→AB|=18.
Dựng điểm I thỏa mãn 2→IA+3→IB+4→IC=→0⇔→AI=13→AB+49→AC.
Khi đó: |2→MA+3→MB+4→MC|=|→MA−→MB| ⇔9|→MI|=18 ⇔IM=2.
Do đó tập hợp các điểm M là đường tròn cố định có bán kính R=2cm.
Hướng dẫn giải:
- Dựng điểm I thỏa mãn 2→IA+3→IB+4→IC=→0
- Tìm vị trí của M theo I.




