Cho tam giác $ABC$ đều cạnh bằng $a$. Tập hợp các điểm $M$ thỏa mãn đẳng thức $4M{A^2} + M{B^2} + M{C^2} = \dfrac{{5{a^2}}}{2}$ nằm trên một đường tròn $\left( C \right)$ có bán kính $R$. Tính \(R\).
Trả lời bởi giáo viên
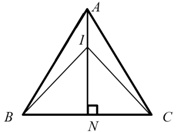
Gọi \(N\) là trung điểm đoạn \(BC\).
Gọi \(I\) là điểm thỏa: \(4\overrightarrow {IA} + \overrightarrow {IB} + \overrightarrow {IC} = \overrightarrow 0 \) \( \Leftrightarrow 4\overrightarrow {IA} + 2\overrightarrow {IN} = \overrightarrow 0 \) \( \Leftrightarrow 2\overrightarrow {IA} + \overrightarrow {IN} = \overrightarrow 0 \), nên điểm \(I\) thuộc đoạn thẳng \(AN\) sao cho \(IN = 2IA\).
Khi đó: \(IA = \dfrac{1}{3}AN = \dfrac{1}{3}.\dfrac{{a\sqrt 3 }}{2} = \dfrac{{a\sqrt 3 }}{6}\), và \(IN = \dfrac{2}{3}AN = \dfrac{2}{3}.\dfrac{{a\sqrt 3 }}{2} = \dfrac{{a\sqrt 3 }}{3}\).
\(I{B^2} = I{C^2} = I{N^2} + B{N^2} = \dfrac{{{a^2}}}{3} + \dfrac{{{a^2}}}{4}\)\( = \dfrac{{7{a^2}}}{{12}}\).
Ta có: $4M{A^2} + M{B^2} + M{C^2} = \dfrac{{5{a^2}}}{2}$\( \Leftrightarrow 4{\left( {\overrightarrow {MI} + \overrightarrow {IA} } \right)^2} + {\left( {\overrightarrow {MI} + \overrightarrow {IB} } \right)^2} + {\left( {\overrightarrow {MI} + \overrightarrow {IC} } \right)^2} = \dfrac{{5{a^2}}}{2}\).
\( \Leftrightarrow 6M{I^2} + 4I{A^2} + I{B^2} + I{C^2} = \dfrac{{a\sqrt 5 }}{2}\) \( \Leftrightarrow 6M{I^2} + 4.\dfrac{{{a^2}}}{{12}} + 2.\dfrac{{7{a^2}}}{{12}} = \dfrac{{5{a^2}}}{2}\) \( \Leftrightarrow MI = \dfrac{a}{{\sqrt 6 }}\).
Hướng dẫn giải:
- Gọi \(N\) là trung điểm đoạn \(BC\).
- Tìm \(I\) là điểm thỏa: \(4\overrightarrow {IA} + \overrightarrow {IB} + \overrightarrow {IC} = \overrightarrow 0 \).
- Tìm \(M\) theo \(I\) và kết luận.




