Câu hỏi:
2 năm trước
Cho tam giác \(ABC\) có \(AB > AC.\) Điểm \(M\) là trung điểm của \(BC.\) Chọn câu đúng.
Trả lời bởi giáo viên
Đáp án đúng: c
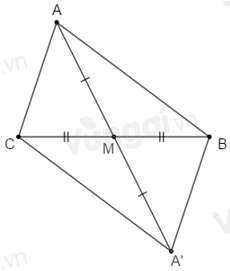
Trên tia đối của tia \(MA\) ta lấy điểm \(A'\) sao cho \(MA = MA'.\)
Xét \(\Delta AMB\) và \(\Delta A'MC\) có:
\(AM = A'M\) (cách vẽ)
\(MB = MC\) (vì \(M\) là trung điểm \(BC\))
\(\widehat {AMB} = \widehat {A'MC}\) (đối đỉnh)
\( \Rightarrow \Delta AMB = \Delta A'MC\,\,(c.g.c)\)
\( \Rightarrow AB = A'C\) (hai cạnh tương ứng)
Xét \(\Delta ACA'\) có: \(A'C - AC < AA' < A'C + AC\) (bất đẳng thức tam giác)
Mà \(AB = A'C\,\,(cmt);\,AA' = 2AM\) (theo cách vẽ) nên ta có:
\(\begin{array}{l}AB - AC < 2AM < AB + AC\\ \Rightarrow \dfrac{{AB - AC}}{2} < AM < \dfrac{{AB + AC}}{2}\end{array}\).
Hướng dẫn giải:
- Trên tia đối của tia \(MA\) ta lấy điểm \(A'\) sao cho \(MA = MA'.\) Chứng minh \(\Delta AMB = \Delta A'MC\,\,(c.g.c)\), suy ra \(AB = A'C\) (hai cạnh tương ứng)
- Áp dụng bất đẳng thức ta có: \(A'C - AC < AA' < A'C + AC\), từ đó lập luận suy ra mối quan hệ cần tìm.
Câu hỏi khác
- Bài tập mối quan hệ giữa đường vuông góc và đường xiên, đường xiên và hình chiếu toán 7 có lời giải
- Bài tập về ba đường trung tuyến của tam giác toán 7 có lời giải
- Bài tập quan hệ giữa góc và cạnh đối diện trong một tam giác toán 7 có lời giải
- Bài tập quan hệ giữa ba cạnh của một tam giác toán 7 có lời giải
- Bài tập về ba đường phân giác của tam giác toán 7 có lời giải
