Câu hỏi:
2 năm trước
Cho parabol \(\left( P \right):y = \dfrac{1}{4}{x^2}\) và đường thẳng \(d:y = \dfrac{{11}}{8}x - \dfrac{3}{2}.\) Gọi \(A,B\) là các giao điểm của \(\left( P \right)\) và \(d.\) Tìm tọa độ điểm \(C\) trên trục tung sao cho \(CA + CB\) có giá trị nhỏ nhất.
Trả lời bởi giáo viên
Đáp án đúng: b
Hoành độ của \(A\) và \(B\) là nghiệm của phương trình: \(\dfrac{1}{4}{x^2} = \dfrac{{11}}{8}x - \dfrac{3}{2}.\)
Phương trình này có hai nghiệm: \(x = 4\) và \(x = \dfrac{3}{2}.\)
Suy ra \(A\left( {4;4} \right),B\left( {\dfrac{3}{2};\dfrac{9}{{16}}} \right).\)
Dễ thấy hai điểm \(A,B\) cùng nằm về một phía so với trục tung ) (do cùng có hoành độ dương).
Lấy điểm \(A'\left( { - 4;4} \right)\) đối xứng với \(A\) qua trục tung.
Khi đó \(CA + CB = CA' + CB \ge A'B\), nên \(CA + CB\) đạt giá trị nhỏ nhất khi và chỉ khi \(A',C,B\) thẳng hàng, tức là khi \(C\) là giao điểm của đường thẳng \(A'B\) với trục tung.
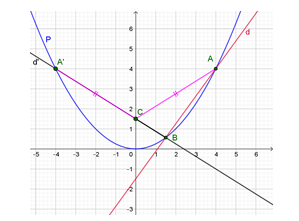
Phương trình đường thẳng \(d'\) đi qua \(A'\) và \(B\) có dạng \(y = ax + b.\)
Ta có hệ \(\left\{ \begin{array}{l}4 = - 4a + b\\\dfrac{9}{{16}} = \dfrac{3}{2}a + b\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = - \dfrac{5}{8}\\b = \dfrac{3}{2}\end{array} \right..\) Suy ra \(d':y = - \dfrac{5}{8}x + \dfrac{3}{2}.\)
Suy ra giao điểm của $(d')$ với trục tung có hoành độ $x=0 \Rightarrow y=\dfrac{3}{2}$
Vậy \(C\left( {0;\dfrac{3}{2}} \right).\)
Hướng dẫn giải:
Lấy \(A'\) đối xứng với \(A\) qua trục tung, khi đó \(CA + CB = CA' + CB \ge A'B\)
Câu hỏi khác
- Bài tập hàm số bậc hai một ẩn và đồ thị hàm số y=ax^2 toán 9 có lời giải
- Bài tập hệ thức vi-ét và ứng dụng toán 9 có lời giải
- Bài tập phương trình bậc hai một ẩn và công thức nghiệm toán 9 có lời giải
- Bài tập công thức nghiệm thu gọn toán 9 có lời giải
- Bài tập phương trình quy về phương trình bậc hai toán 9 có lời giải
