Câu hỏi:
2 năm trước
Cho hình vuông \(ABCD\) có cạnh \(2R.\)
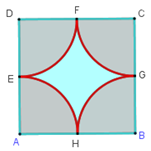
Diện tích \(S\) phần màu xanh trong hình vuông \(ABCD\) là
Trả lời bởi giáo viên
Đáp án đúng: a
Gọi \(S,\,{S_1},\,{S_2}\) lần lượt là diện tích phần màu xanh, diện tích hình vuông và diện tích phần còn lại.
Khi đó ta có \({S_1} = {\left( {2R} \right)^2}=4R^2\,\,\left( 1 \right).\)
Nhận thấy mỗi hình quạt \(AEH,BHG,CGF,DFE\) là \(\dfrac{1}{4}\) hình tròn bán kính \(R= \dfrac{{AB}}{2}\)
Nên tổng diện tích \(4\) hình quạt \(AEH,BHG,CGF,DFE\) chính bằng diện tích của hình tròn bán kính $R$ .
Hay \({S_2} = \pi {R^2}\,\,\left( 2 \right).\)
Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) ta suy ra \(S = 4{R^2} - \pi {R^2}.\)
Hướng dẫn giải:
Tính các diện tích hình vuông \(ABCD\), các hình quạt \(AEH,BHG,CGF,DFE\).
Diện tích phần màu xanh là hiệu giữa diện tích hình vuông và các hình quạt.
