Cho hình thang cân \(ABCD\) có đáy nhỏ \(AB\), đáy lớn \(CD\). Biết \(AB = AD\) và \(\tan \widehat {BDC} = \dfrac{3}{4}\). Tính $\cos \widehat {BAD}$.
Trả lời bởi giáo viên
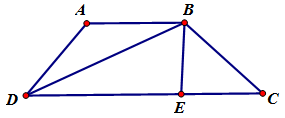
Gọi $E$ là hình chiếu vuông góc của \(B\) trên $DC$. Đặt $AB = AD = BC = x$.
Ta có \(EC = \dfrac{{DC - x}}{2}\) \(\left( 1 \right)\).
Trong tam giác vuông \(BDE\) ta có: \(\tan \widehat {BDC} = \dfrac{3}{4}\) \( \Leftrightarrow \) \(\dfrac{{BE}}{{ED}} = \dfrac{3}{4}\) \( \Leftrightarrow \) \(BE = \dfrac{3}{4}ED\)
\( \Leftrightarrow \) \(BE = \dfrac{3}{4}\left( {DC - \dfrac{{DC - x}}{2}} \right)\)\( = \dfrac{3}{8}\left( {DC + x} \right)\) \(\left( 2 \right)\).
Trong tam giác vuông \(BEC\) ta có \(B{C^2} = E{C^2} + B{E^2}\) \(\left( 3 \right)\).
Thay \(\left( 1 \right)\), \(\left( 2 \right)\) vào \(\left( 3 \right)\) biến đổi ta được: \(39{x^2} + 14DC.\,x - 25D{C^2} = 0\) \( \Leftrightarrow \) \(x = \dfrac{{25}}{{39}}DC\) hay \(DC = \dfrac{{39}}{{25}}x\). Khi đó \(EC = \dfrac{7}{{25}}x\).
Mặt khác: $\cos \widehat {BAD}$\( = - \cos \widehat {BCE}\)\( = - \dfrac{{EC}}{{BC}} = - \dfrac{7}{{25}}\)
Hướng dẫn giải:
- Gọi $E$ là hình chiếu vuông góc của \(B\) trên $DC$. Đặt $AB = AD = BC = x$.
- Tính \(EC\) theo \(x\) suy ra \(\cos \widehat {BCD}\) và \(\cos \widehat {BAD} = - \cos \widehat {BCD}\)




