Câu hỏi:
2 năm trước
Cho hình hộp chữ nhật \(ABCD.A'B'C'D'\) có \(AB = 4,{\rm{ }}AD = 3.\) Mặt phẳng \((ACD')\) tạo với mặt đáy một góc \({60^ \circ }.\) Tính khoảng cách giữa hai mặt đáy của hình hộp.
Trả lời bởi giáo viên
Đáp án đúng: b
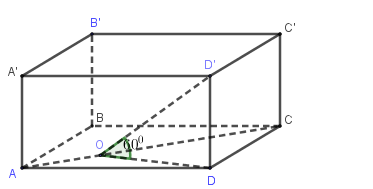
Gọi \(O\) là hình chiếu của \(D\) lên \(AC\).
Ta có \(\left\{ \begin{array}{l}\left( {ACD'} \right) \cap \left( {ABCD} \right) = AC\\AC \bot DO\\AC \bot D'O\left( {AC \bot \left( {ODD'} \right) \supset OD'} \right)\end{array} \right.\)
\( \Rightarrow \left( {\widehat {\left( {D'AC} \right),\left( {ABCD} \right)}} \right) = \widehat {D'OD} = {60^0}\)
\(AC = \sqrt {{3^2} + {4^2}} = 5\) ; \(DO = \dfrac{{AD.DC}}{{AC}} = \dfrac{{12}}{5}\)
Khoảng cách giữa hai mặt đáy là \(DD' = DO.\tan {60^0} = \dfrac{{12\sqrt 3 }}{5}\)
Hướng dẫn giải:
- Xác định góc giữa hai mặt phẳng \(\left( {ACD'} \right)\) và \(\left( {ABCD} \right)\) theo dấu hiệu: góc giữa hai mặt là góc giữa hai đường thẳng nằm trong hai mặt phẳng và cùng vuông góc với giao tuyến tại một điểm.
- Khoảng cách giữa hai mặt đáy của hình hộp chữ nhật chính là độ dài cạnh bên của hình hộp.
