Câu hỏi:
3 năm trước
Cho hình hộp $ABCD.A'B'C'D'$ có đáy là hình thoi $\widehat {BAD} = {60^0}$ và $A'A = A'B = A'D$. Gọi $O = AC \cap BD$. Hình chiếu của $A'$ trên $\left( {ABCD} \right)$ là :
Trả lời bởi giáo viên
Đáp án đúng: b
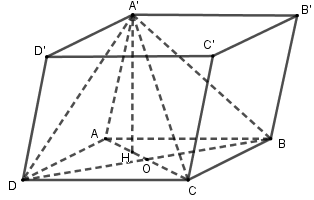
Vì $A'A = A'B = A'D \Rightarrow $ hình chiếu của \(A'\) trên $\left( {ABCD} \right)$ trùng với \(H\) là tâm đường tròn ngoại tiếp \(\Delta ABD\,\,\left( 1 \right).\)
Mà tứ giác \(ABCD\) là hình thoi và $\widehat {BAD} = {60^0}$ nên \(\Delta BAD\) là tam giác đều \(\left( 2 \right)\)
Từ \(\left( 1 \right)\,\)và \(\left( 2 \right) \Rightarrow H\) là trọng tâm \(\Delta ABD\,.\)
Hướng dẫn giải:
Sử dụng định nghĩa trục đường tròn đáy để tìm hình chiếu của \(A'\) trên mặt đáy

