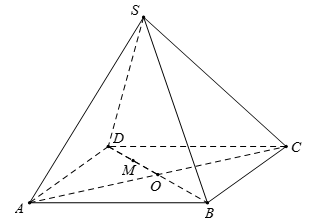
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông tâm $O$, tam giác $SBD$  cân tại $S$. Gọi $M$ là điểm tùy ý trên $AO$. Mặt phẳng \(\left( \alpha  \right)\) đi qua $M$ và song song với $SA,BD$  cắt $SO,SB,AB$ tại $N,P,Q$. Tứ giác $MNPQ$  là hình gì?

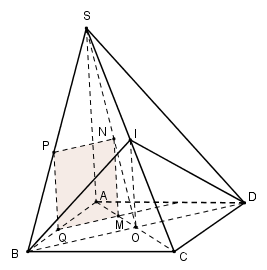
Tam giác $SBD$ cân tại $S$  nên $SB = SD$ .

Suy ra \(\Delta SBC = \Delta SDC\left( {c.c.c} \right) \Rightarrow \widehat {SCB} = \widehat {SCD}\).

Gọi $I$  là trung điểm của $SC$ .

Xét hai tam giác $IBC$  và $ICD$  có:

$IC$ chung

$BC = DC$ ($ABCD$ là hình vuông)

\(\widehat {ICB} = \widehat {ICD}\,\left( {cmt} \right)\)

Do đó \(\Delta IBC = \Delta IDC\left( {c.g.c} \right) \Rightarrow IB = ID\) hay tam giác $ICD$  cân tại $I$ .

Do $O$  là trung điểm của $BD$  nên $IO$  là đường trung tuyến trong tam giác cân \( \Rightarrow IO \bot BD.\)

Mà $SA//IO$ nên \(SA \bot BD.\)

Ta có: \(\left\{ \begin{array}{l}M \in \left( \alpha  \right) \cap \left( {ABCD} \right)\\BD\parallel \left( \alpha  \right)\\BD \subset \left( {ABCD} \right)\end{array} \right.\)

Suy ra giao tuyến của \(\left( \alpha  \right)\) với $\left( {ABCD} \right)$  là đường thẳng qua $M$  và song song với $BD$  cắt $AB$  tại $Q$ \( \Rightarrow MQ\parallel BD.\,\,\left( 1 \right)\)

Ta có: \(\left\{ \begin{array}{l}Q \in \left( \alpha  \right) \cap \left( {SAB} \right)\\SA\parallel \left( \alpha  \right)\\SA \subset \left( {SAB} \right)\end{array} \right.\) suy ra giao tuyến của \(\left( \alpha  \right)\)với $\left( {SAB} \right)$  là đường thẳng đi qua $Q$  và song song với $SA$  cắt $SB$ tại $P$ . Do đó $QP//SA\left( 2 \right)$

Ta có: \(\left\{ \begin{array}{l}P \in \left( \alpha  \right) \cap \left( {SBD} \right)\\BD\parallel \left( \alpha  \right)\\BD \subset \left( {SBD} \right)\end{array} \right.\)suy ra giao tuyến của \(\left( \alpha  \right)\)với $\left( {SBD} \right)$  là đường thẳng đi qua $P$ và song song với $BD$  cắt $SO$  tại $N$ . Do đó $PN//BD\left( 3 \right)$ .

Ta có: \(\left\{ \begin{array}{l}\left( \alpha  \right) \cap \left( {SAC} \right) = MN\\SA\parallel \left( \alpha  \right)\\SA \subset \left( {SAC} \right)\end{array} \right. \Rightarrow MN\parallel SA.\) (4).

Từ (1) và (3) suy ra $PN//MQ//BD$ , từ (2) và (4) suy ra $QP//MN//SA$ . Do đó $MNPQ$ là hình bình hành.

Lại có \(SA \bot BD \Rightarrow MN \bot MQ\) .

Vậy $MNPQ$  là hình chữ nhật.