Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành. Gọi \(M,\,\,N\) lần lượt là trung điểm của các cạnh \(AB,\,\,BC\). Điểm \(I\) thuộc đoạn \(SA\). Biết mặt phẳng \(\left( {MNI} \right)\) chia khối chóp \(S.ABCD\)  thành hai phần, phần chứa đỉnh \(S\) có thể tích bằng \(\dfrac{7}{{25}}\) lần phần còn lại. Tính tỉ số \(\dfrac{{IA}}{{IS}}\)?

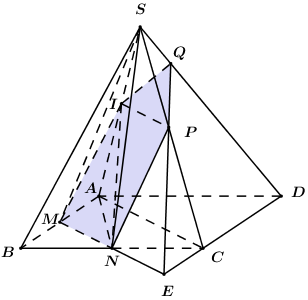
Giả sử \(SC \cap \left( {IMN} \right) = \left\{ P \right\}\) \( \Rightarrow \left( {IMN} \right) \cap \left( {SAC} \right) = IP\).

Ta có: \(\left\{ \begin{array}{l}\left( {IMN} \right) \cap \left( {SAC} \right) = IP\\\left( {IMN} \right) \cap \left( {ABCD} \right) = MN\\\left( {SAC} \right) \cap \left( {ABCD} \right) = AC\end{array} \right. \Rightarrow IP\parallel MN\parallel AC\).

Trong \(\left( {ABCD} \right)\) gọi \(\left\{ E \right\} = MN \cap CD\), trong \(\left( {SCD} \right)\) goji \(Q = NP \cap SD\).

Khi đó thiết diện của hình chóp cắt bởi \(\left( {MNI} \right)\) là ngũ giác \(IMNPQ\).

Gọi \({V_1} = {V_{S.BMNPQI}},\,\,V = {V_{S.ABCD}}\), theo bài ra ta có \({V_1} = \dfrac{7}{{32}}V\).

Ta có \({V_1} = {V_{S.BMN}} + {V_{S.IMN}} + {V_{S.INP}} + {V_{S.IPQ}}\).

Đặt \(\dfrac{{SI}}{{SA}} = x\,\,\,\left( {0 < x < 1} \right)\), áp dụng định lí Ta-lét ta có \(\dfrac{{SI}}{{SA}} = \dfrac{{SP}}{{SC}} = x\).

- Xét khối chóp \(S.BMN\) và \(S.ABCD\):

  + Có cùng chiều cao (cùng bằng khoảng cách từ \(S\) đến \(\left( {ABCD} \right)\)).

  + \({S_{BMN}} = \dfrac{1}{4}{S_{ABC}} = \dfrac{1}{8}{S_{ABC}}\) (do tam giác \(BMN\) và tam giác \(BAC\) đồng dạng theo tỉ số \(\dfrac{1}{2}\))

Do đó \({V_{S.BMN}} = \dfrac{1}{8}{V_{S.ABCD}} = \dfrac{1}{8}V\).

- Xét khối chóp \(S.IMN\) và \(S.AMN\):

   \(\dfrac{{{V_{S.IMN}}}}{{{V_{S.AMN}}}} = \dfrac{{SI}}{{SA}} = x \Rightarrow {V_{S.IMN}} = x.{V_{S.AMN}}\).

Ta có \({S_{AMN}} = {S_{BMN}} = \dfrac{1}{8}{S_{ABCD}}\) \( \Rightarrow {V_{S.AMN}} = \dfrac{1}{8}V\) \( \Rightarrow {V_{S.IMN}} = \dfrac{x}{8}V\).

- Xét khối chóp \(S.INP\) và \(S.ANC\):

   \(\dfrac{{{V_{S.INP}}}}{{{V_{S.ANC}}}} = \dfrac{{SI}}{{SA}}.\dfrac{{SP}}{{SC}} = {x^2} \Rightarrow {V_{S.IMN}} = {x^2}.{V_{S.ANC}}\).

Ta có \({S_{ANC}} = \dfrac{1}{2}{S_{ABC}} = \dfrac{1}{4}{S_{ABCD}}\) \( \Rightarrow {V_{S.ANC}} = \dfrac{1}{4}V\) \( \Rightarrow {V_{S.IMN}} = \dfrac{{{x^2}}}{4}V\).

- Xét khối chóp \(S.IPQ\) và \(S.ACD\): \(\dfrac{{{V_{S.IPQ}}}}{{{V_{S.ACD}}}} = \dfrac{{SI}}{{SA}}.\dfrac{{SP}}{{SC}}.\dfrac{{SQ}}{{SD}}\).

Ta có \(AMEC\) là hình bình hành nên \(EC = AM = \dfrac{1}{2}CD \Rightarrow \dfrac{{EC}}{{ED}} = \dfrac{1}{3}\).

Áp dụng định lí Menelaus trong tam giác \(SCD\) với cát tuyến \(EPQ\) ta có:

\(\dfrac{{PS}}{{PC}}.\dfrac{{EC}}{{ED}}.\dfrac{{QD}}{{QS}} = 1\) \( \Rightarrow \dfrac{x}{{1 - x}}.\dfrac{1}{3}.\dfrac{{QD}}{{QS}} = 1\)

\(\begin{array}{l} \Rightarrow \dfrac{{QD}}{{QS}} = \dfrac{{3\left( {1 - x} \right)}}{x} \Rightarrow \dfrac{{SQ}}{{QD}} = \dfrac{x}{{3\left( {1 - x} \right)}}\\ \Rightarrow \dfrac{{SQ}}{{SQ + QD}} = \dfrac{x}{{x + 3\left( {1 - x} \right)}}\\ \Rightarrow \dfrac{{SQ}}{{SD}} = \dfrac{x}{{3 - 2x}}\end{array}\)

Suy ra \(\dfrac{{{V_{S.IPQ}}}}{{{V_{S.ACD}}}} = \dfrac{{SI}}{{SA}}.\dfrac{{SP}}{{SC}}.\dfrac{{SQ}}{{SD}} = {x^2}.\dfrac{x}{{3 - 2x}} = \dfrac{{{x^3}}}{{3 - 2x}}\)\( \Rightarrow {V_{S.IPQ}} = \dfrac{{{x^3}}}{{3 - 2x}}{V_{S.ACD}}\).

Mà \({S_{ACD}} = \dfrac{1}{2}{S_{ABCD}} \Rightarrow {V_{S.ACD}} = \dfrac{1}{2}V\) \( \Rightarrow {V_{S.IPQ}} = \dfrac{{{x^3}}}{{2\left( {3 - 2x} \right)}}V\).

Khi đó ta có:

\(\begin{array}{l}\,\,\,\,\,\,{V_1} = {V_{S.BMN}} + {V_{S.IMN}} + {V_{S.INP}} + {V_{S.IPQ}}\\ \Rightarrow {V_1} = \dfrac{1}{8}V + \dfrac{x}{8}V + \dfrac{{{x^2}}}{4}V + \dfrac{{{x^3}}}{{2\left( {3 - 2x} \right)}}V\\ \Rightarrow {V_1} = \left( {\dfrac{1}{8} + \dfrac{x}{8} + \dfrac{{{x^2}}}{4} + \dfrac{{{x^3}}}{{2\left( {3 - 2x} \right)}}} \right)V = \dfrac{7}{{32}}V\\ \Rightarrow \dfrac{1}{8} + \dfrac{x}{8} + \dfrac{{{x^2}}}{4} + \dfrac{{{x^3}}}{{2\left( {3 - 2x} \right)}} = \dfrac{7}{{32}}\\ \Leftrightarrow \dfrac{{1 + x + 2{x^2}}}{4} + \dfrac{{{x^3}}}{{3 - 2x}} = \dfrac{7}{{16}}\\ \Leftrightarrow \left( {1 + x + 2{x^2}} \right).\left( {12 - 8x} \right) + 16{x^3} = 7\left( {3 - 2x} \right)\\ \Leftrightarrow 12 + 12x + 24{x^2} - 8x - 8{x^2} - 16{x^3} + 16{x^3} = 21 - 14x\\ \Leftrightarrow 16{x^2} + 18x - 9 = 0 \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{3}{8}\,\,\,\,\,\,\,\left( {tm} \right)\\x =  - \dfrac{3}{2}\,\,\left( {ktm} \right)\end{array} \right.\end{array}\)

\( \Rightarrow \dfrac{{SI}}{{SA}} = \dfrac{3}{8} \Rightarrow \dfrac{{IS}}{{IA}} = \dfrac{3}{5} \Rightarrow \dfrac{{IA}}{{IS}} = \dfrac{5}{3}\).