Câu hỏi:
2 năm trước
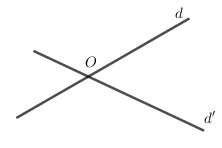
Cho hai đường thẳng cắt nhau $d$ và $d'$. Có bao nhiêu phép đối xứng tâm biến mỗi đường thẳng đó thành chính nó
Trả lời bởi giáo viên
Đáp án đúng: b
Qua một phép đối xứng tâm, đường thẳng biến thành chính nó khi và chỉ khi tâm đối xứng là điểm thuộc đường thẳng nó.
Gọi $O$ là tâm đối xứng sao cho qua phép đối xứng tâm $O$ biến mỗi đường thẳng $d$ và $d'$ thành chính nó.
\( \Rightarrow \left\{ \begin{array}{l}O \in d\\O \in d'\end{array} \right. \Rightarrow O = d \cap d'\) và $O$ là duy nhất.
Hướng dẫn giải:
Qua một phép đối xứng tâm, đường thẳng biến thành chính nó khi và chỉ khi tâm đối xứng là điểm thuộc đường thẳng nó.

