Câu hỏi:
3 năm trước
Cho đường tròn \(\left( O \right)\) Trên \(\left( O \right)\) lấy ba điểm \(A,B,D\) sao cho \(\widehat {AOB} = {120^0},\,\,AD = BD.\)
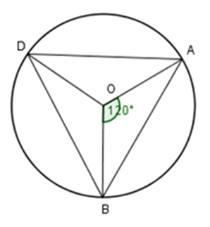
Khi đó \(\Delta ABD\) là:
Trả lời bởi giáo viên
Đáp án đúng: a
Từ mối liên hệ về số đo góc ở tâm và số đo góc nội tiếp ta có
$\widehat {ADB} = \dfrac{1}{2}\widehat {AOB} = \dfrac{1}{2}{.120^0} = {60^0}.$
\(\Delta ABD\) có \(AD = BD\) nên cân tại \(D,\) có một góc $\widehat {ADB}=60^0$ nên \(\Delta ABD\) là tam giác đều.
Hướng dẫn giải:
Sử dụng mối liên hệ về số đo góc ở tâm và số đo góc nội tiếp để tính góc $\widehat {ADB}$ của tam giác $ABD$
Từ đó dựa vào điều kiện đề bài để suy ra tính chất tam giác $ABD$


