Cho đường tròn \(\left( {O;R} \right)\) và dây cung \(BC = R.\) Hai tiếp tuyến của đường tròn \(\left( O \right)\) tại \(B,C\) cắt nhau tại \(A.\) Gọi \(M\) là giao điểm của \(AO\) và \(BC.\) Khi đó tam giác \(AMB\) là:

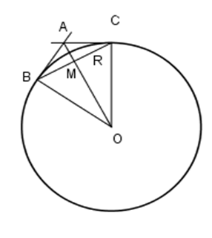
Xét đường tròn $(O)$ có dây \(BC = R = OC = OB\) nên \(\Delta BOC\) là tam giác đều. Do đó

\(\widehat {BOC} = {60^0} \Rightarrow \) sđ \(\overparen{BC} = {60^0}\)

Lại có \(\widehat {ABC}\) là góc tạo bởi hai tiếp tuyến \(BA\) và dây cung \(BC\) của \(\left( O \right).\)

Do góc tạo bởi tia tiếp tuyến và dây cung bằng nửa số đo cung bị chắn nên \(\widehat {ABC} = \dfrac{1}{2}\) sđ \(\overparen{BC} = {30^0}\).

Lại có $AB=AC$ (tính chất hai tiếp tuyến cắt nhau) và $OB=OC=R$ nên $AO$ là đường trung trực của $BC$

Hay $AO \bot BC$ tại $M$, suy ra \(\widehat {AMB} = {90^0} \Rightarrow \widehat {BAM} = {60^0}.\)

Như vậy tam giác $AMB$ vuông tại $M$ và có \(\widehat {ABM} = {30^0};\, \widehat {BAM} = {60^0}\)

Nên đáp án A, B đều đúng.

Ta lại có \(\sin \widehat {ABM} = \dfrac{{AM}}{{AB}} \Rightarrow \dfrac{{AM}}{{AB}} = \sin \,{30^0} = \dfrac{1}{2}.\)

Hay cạnh góc vuông \(AM\) bằng nửa cạnh huyền \(AB.\) Vì vậy đáp án C cũng đúng.