Cho đường tròn \(\left( {O;R} \right)\) và dây cung  \(AB\) không đi qua \(O\).  Từ điểm \(M\) nằm trên tia đối của tia \(BA\)

 (\(M\) không trùng với \(B\)), kẻ hai tiếp tuyến \(MC,MD\) với đường tròn \(\left( {O;R} \right)\)(\(C;D\) là các tiếp điểm). Gọi \(H\) là trung điểm đoạn thẳng \(AB\). Đoạn thẳng \(OM\) cắt đường tròn \(\left( {O;R} \right)\) tại điểm \(I\).

Chọn câu sai.

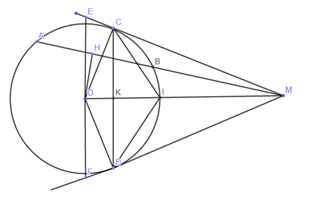
* Xét đường tròn \(\left( {O;R} \right)\) có \(H\) là trung điểm của dây cung \(AB\)\( \Rightarrow OH \bot AB \Rightarrow \angle OHM = {90^o}\) (mối liên hệ giữa đường kính và dây cung)

Xét đường tròn \(\left( {O;R} \right)\) có \(MD\) là tiếp tuyến \( \Rightarrow OD \bot MD \Rightarrow \angle ODM = {90^o}\) (tính chất của tiếp tuyến)

Xét tứ giác \(DOHM\) có: \(\left\{ \begin{array}{l}\angle OHM = {90^o}\\\angle ODM = {90^o}\end{array} \right. \Rightarrow \angle OHM + \angle ODM = {180^o}\)

Suy ra tứ giác \(DOHM\) nội tiếp đường tròn  \( \Rightarrow D;O;H;M\) cùng thuộc một đường tròn nên A đúng.

* Xét \(\Delta COM\) và \(\Delta DOM\) có

+)\(OM\) chung

+) \(\angle OCM = \angle ODM = {90^o}\)

+) \(OC = OD = R\)

\( \Rightarrow \Delta COM = \Delta DOM\) (cạnh huyền - cạnh góc vuông) \( \Rightarrow \angle COI = \angle IOD\) (2 góc tương ứng)

\( \Rightarrow CI = ID \Rightarrow \Delta ICD\) cân \( \Rightarrow \angle ICD = \angle IDC\) (Tính chất tam giác cân) 

Xét đường tròn \(\left( {O;R} \right)\) có \(\angle ICD\) là góc nội tiếp chắn cung \(ID\); \(\angle IDM\) là góc tạo bởi tiếp tuyến và dây cung chắn cung \(ID\)\( \Rightarrow \angle ICD = \angle IDM\)

Mà có \(\angle ICD = \angle IDC \Rightarrow \angle IDO = \angle IDM\)

\( \Rightarrow ID\) là phân giác \(\angle ODM\)                                            (1)

Chứng minh tương tự có : \(IC\) là phân giác \(\angle MCO\)\(\)  (2)

Mà có \(ID\) cắt \(IC\) tại \(I\), suy ra \(I\) là giao điểm của 3 đường phân giác trong \(\Delta MCD\). Suy ra \(I\) là tâm đường tròn nội tiếp \(\Delta MCD\) nên B đúng, C sai.