Cho đường tròn \(\left( {O;R} \right),\) đường kính \(AB\) cố định, đường kính \(CD\) thay đổi \(\left( {CD \ne AB} \right).\) Các tia \(BC,\,BD\) cắt tiếp tuyến của đường tròn \(\left( O \right)\) tại \(A\) lần lượt tại \(E,\,F.\)

Tứ giác \(DCEF\) là

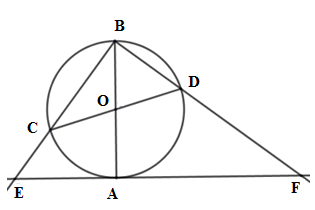
Xét \(\left( O \right)\) có \(AB;CD\) là các đường kính nên \(\widehat {CBD} = 90^\circ \)

Xét tam giác \(BCD\) vuông tại \(B\) có \(\widehat {BCD} + \widehat {BDC} = 90^\circ \) mà \(\widehat {OBD} = \widehat {ODB}\)  (do \(\Delta OBD\) cân tại \(O\) )

Nên \(\widehat {BCD} + \widehat {OBD} = 90^\circ  \Rightarrow \widehat {BCD} = 90^\circ  - \widehat {OBD}\)  (1)

Xét tam giác \(ABF\) vuông tại \(A\) (vì $EF$ là tiếp tuyến của $(O)$) có \(\widehat {BFA} = 90^\circ  - \widehat {ABF}\)  (2)

Từ (1) và (2) suy ra \(\widehat {BCD} = \widehat {DFA}\)

Do đó tứ giác \(DCEF\) là tứ giác nội tiếp (dấu hiệu góc ngoài tại một đỉnh bằng góc trong tại đỉnh đối với đỉnh đó)