Cho đường tròn (O) bán kính R ngoại tiếp tam giác ABC có ba góc nhọn. Các tiếp tuyến của đường tròn (O) tại các điểm B, C cắt nhau tại điểm P. Gọi D, E tương ứng là chân các đường vuông góc hạ từ P xuống  các đường thẳng AB, AC và M là trung điểm cạnh BC.

Đường thẳng \(DE\)  đi qua điểm cố định nào ?

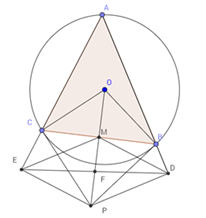
\(\;\widehat {A\;} = \;\widehat {CBP}\;\) cùng chắn cung \(BC\)

Ta có. \(\widehat A\) + \(\widehat {ABC}\) + \(\widehat {ACB} = {180^0}\;\) (tổng ba góc trong tam giác)

Có \(\widehat {CBP}\) + \(\widehat {ABC}\;\)+ \(\widehat {PBD}\) = \({180^0}\) (vì A, B, D thẳng hàng)

\( \Rightarrow \widehat {ACB}\;\)=  \(\widehat {PBD}\)

Mà \(\widehat {ACB}\;\) = \(\widehat {MPE}\) (cùng phụ góc $ECM$ )

\(\widehat {PBD}\) = \(\widehat {MPE}\)(cùng chắn cung $BD$ )

=> \(\widehat {MPE}\;\)= \(\widehat {MPE}\)

Mà 2 góc trên ở vị trí so le trong  \( \Rightarrow MD//EP\)

Mặt khác ta xét hai tam giác  \(\Delta MEP\;;\;\Delta PDM\)  ta chứng minh được \(\widehat {EMP} = \;\widehat {MPD}\)

Mà 2 góc lại ở vị trí so le trong  nên  \(ME//PD\)

Vậy tứ giác $EMDP$ là hình bình hành

\( \Rightarrow ED\)  đi qua trung điểm $F$ của $MP$

Vì $B,{\rm{ }}C$ cố định \( \Rightarrow M,P\) cố định \( \Rightarrow \)  trung điểm $F$ của $MP$ cố định