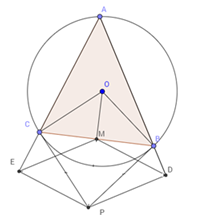
Cho đường tròn (O) bán kính R ngoại tiếp tam giác ABC có ba góc nhọn. Các tiếp tuyến của đường tròn (O) tại các điểm B, C cắt nhau tại điểm P. Gọi D, E tương ứng là chân các đường vuông góc hạ từ P xuống  các đường thẳng AB, AC và M là trung điểm cạnh BC.

Góc \(MEP\)  bằng với góc nào dưới đây?

Ta có M là trung điểm của cạnh BC $ \Rightarrow OM \bot BC$ (liên hệ đường kính và dây cung)

Ta có tứ giác BMPD nội tiếp ( vì \(\widehat {BDP}\)+ \(\widehat {BMP}\)=180⁰) \( \Rightarrow \widehat {MDP}\) = \(\widehat {MBP}\)  (tính chất của tứ giác nội tiếp) (1)

Tương tự có tứ giác  MCEP nội tiếp => \(\widehat {MEP}\) = \(\widehat {MCP}\)  (tính chất của tứ giác nội tiếp) (2)

Mà tiếp tuyến tại B và C cắt nhau tại P  nên dễ dàng suy ra được \(\Delta BPC\;\)cân tại P ( tính chất 2 tiếp tuyến cắt nhau)

\( \Rightarrow \widehat {MCP}{\rm{\;}} = \;\widehat {MBP}\;\left( 3 \right)\)

Từ (1); (2);(3) => \(\widehat {MEP}\) = \(\widehat {MDP}\)