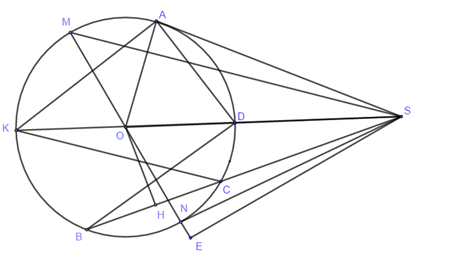
Cho điểm $S$ cố định ở bên ngoài đường tròn \(\left( O \right)\). Vẽ tiếp tuyến $SA$ của đường tròn \(\left( O \right)\) (với A là tiếp điểm) và cát tuyến  $SCB$ không qua tâm  $O,$ điểm $O$ nằm trong \(\widehat {BSA}\), điểm $C$ nằm giữa $S$ và $B.$ Gọi $H$ là trung điểm đoạn thẳng $CB.$

Chọn câu đúng.

Gọi \(D,K\) lần lượt là giao điểm của \(SO\) với đường tròn (\(D\) nằm giữa \(K\) và \(S\))

Xét đường tròn \(\left( O \right)\) có:

 \(\angle SAD\) là góc tạo bởi tiếp tuyến và dây cung chắn cung \(AD\)

\(\angle AKS\) là góc nội tiếp chắn cung \(AD\).

Suy ra \(\angle SAD = \angle AKS\).

Xét \(\Delta SDA\) và $\Delta SAK$ có:

\(\angle KSA\) chung

\(\angle SAD = \angle AKS\) (cmt)

\( \Rightarrow \Delta SDA \backsim \Delta SAK \Rightarrow \dfrac{{SA}}{{SK}} = \dfrac{{SD}}{{SA}} \Rightarrow S{A^2} = SK.SD\).  (1)

Xét \(\Delta KCS\) và \(\Delta BDS\) ta có:

\(\angle AKC = \angle DBS\) (hai góc nội tiếp cùng chắn cung DC)

\(\angle DSC\) chung

\( \Rightarrow \Delta KCS \backsim \Delta BDS \Rightarrow \dfrac{{KS}}{{BS}} = \dfrac{{SC}}{{SD}} \Rightarrow SB.SC = SK.SD\)                         (2)

Từ (1) và (2) \( \Rightarrow S{A^2} = SC.SB\)