Chiếu một chùm sáng hẹp tới mặt trên của một chậu nước dưới góc tới \(i = {60^0}\) chiết suất của nước với ánh sáng đỏ và tím là \({n_d} = 1,31\) ; \({n_t} = 1,38\). Độ sâu của lớp nước là \(30cm\), đáy chậu đặt một gương phẳng nằm ngang, bề rộng dải quang phổ liên tục thu được ở ngoài không khí:
Trả lời bởi giáo viên
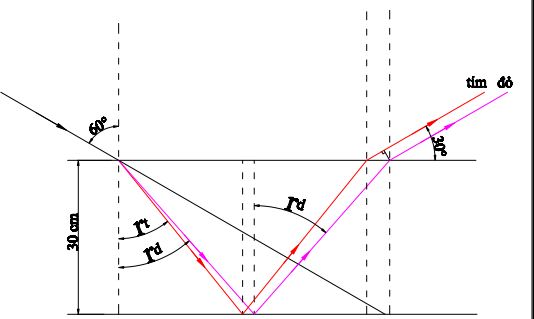
Áp dụng định luật khúc xạ ánh sáng ta tính được
\(sini = {n_d}sin{\rm{ }}{r_d} \to sin{\rm{ }}{r_d} = \frac{{sin{\rm{ }}i}}{{{n_d}}} = \frac{{sin{\rm{ }}{{60}^0}}}{{1,31}} \to {r_d} = {41,38^0}\)
\(sin{\rm{ }}i = {n_t}sin{\rm{ }}{r_t} \to sin{\rm{ }}{r_t} = {\rm{ }}\frac{{sin{\rm{ }}i}}{{{n_t}}}{\rm{ = }}\frac{{sin{\rm{ }}{{60}^0}}}{{1,38}} \to {\rm{ }}{r_t} = {\rm{ }}{38,87^0}\)
Từ hình vẽ trên ta thấy:
Bề rộng quang phổ tại mặt nước được tính theo công thức: \(L = 2h\left( {tan{\rm{ }}{r_d}-{\rm{ }}tan{\rm{ }}{r_t}} \right) = 4,5{\rm{ }}cm\)
=> Bề rộng quang phổ trong không khí là \(d{\rm{ }} = {\rm{ }}Lsin{\rm{ }}{30^0} = {\rm{ }}2,25cm\)
Hướng dẫn giải:
Sử dụng lí thuyết về tán sắc ánh sáng
Định luật khúc xạ ánh sáng: \({n_1}sini{\rm{ }} = {\rm{ }}{n_2}sinr\)