Chiều cao của $1$ tam giác vuông là $8cm$ chia cạnh huyền thành $2$ đoạn thẳng hơn kém nhau $12cm$. Tính độ dài cạnh huyền của tam giác vuông đó.
Trả lời bởi giáo viên
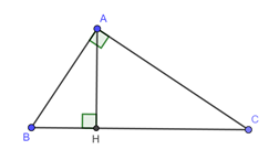
Giả sử tam giác vuông $ABC$ có đường cao $AH$ chia cạnh $BC$ thành $2$ đoạn thẳng $BH$ và $CH$ .
Gọi độ dài cạnh $BH$ là $x{\rm{ }}\left( {cm} \right){\rm{ }}\left( {x > 0} \right)$
Khi đó độ dài cạnh $CH$ là $x + 12\left( {cm} \right)$
Áp dụng hệ thức lượng trong tam giác vuông $ABC$ ta có:
$A{H^2} = BH.CH \Leftrightarrow {8^2} = x(x + 12)$
$ \Leftrightarrow {x^2} + 12x - 64 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 4(tmdk)\\x = - 16(ktmdk)\end{array} \right.$
Suy ra $BH = 4cm$ và $CH = 16cm$
Vậy cạnh huyền $BC = 20cm$.
Hướng dẫn giải:
Các bước giải bài toán bằng cách lập phương trình:
Bước 1: Lập phương trình
1) Chọn ẩn, đơn vị và tìm điều kiện của ẩn (thông thường ẩn là đại lượng bài toán yêu cầu tìm)
2) Biểu thị các đại lượng chưa biết theo ẩn và các đại lượng đã biết
3) Lập phương trình biểu thị mối quan hệ giữa các đại lượng.
Bước 2: Giải phương trình
Sử dụng các phương pháp phân tích đa thức thành nhân tử, giải phương trình bậc nhất, bậc hai…
Bước 3: Kết luận

