Tìm kiếm
Câu hỏi:
2 năm trước

Bất phương trình : $\left| {3x - 3} \right| \le \left| {2x + 1} \right|$ có nghiệm là

a.

\(\left[ {4; + \,\infty } \right).\)
b.

\(\left( { - \,\infty ;\dfrac{2}{5}} \right].\)
c.

\(\left[ {\dfrac{2}{5};4} \right].\)
d.

\(\left( { - \,\infty ;4} \right].\)
Xem đáp án
50 lượt xem
BẮT ĐẦU THI THỬ

Trả lời bởi giáo viên

Đáp án đúng: c

Ta có $\left| {3x - 3} \right| \le \left| {2x + 1} \right| \Leftrightarrow {\left| {3x - 3} \right|^2} \le {\left| {2x + 1} \right|^2} \Leftrightarrow {\left( {3x - 3} \right)^2} - {\left( {2x + 1} \right)^2} \le 0$

$ \Leftrightarrow \left( {3x - 3 - 2x - 1} \right)\left( {3x - 3 + 2x + 1} \right) \le 0 \Leftrightarrow \left( {x - 4} \right)\left( {5x - 2} \right) \le 0 $

Xét dấu \(\left( {x - 4} \right)\left( {5x - 2} \right)\) ta được:

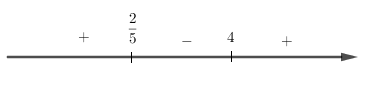
Suy ra $\dfrac{2}{5} \le x \le 4$

Vậy tập nghiệm của bất phương trình là $S = \left[ {\dfrac{2}{5};4} \right].$

Hướng dẫn giải:

- Bình phương hai vế (đều dương), rút gọn đưa về tích các nhị thức bậc nhất.

- Xét dấu vế trái và kết luận nghiệm.

Câu hỏi khác

Câu 1:

Tập nghiệm của bất phương trình \(\left| {2x + 3} \right| - \left| {3x - 4} \right| \ge  - 5\) có độ dài bằng

\(\dfrac{{32}}{5}\)

\(\dfrac{{16}}{5}\)

\(\dfrac{{64}}{5}\)

\(\dfrac{{4}}{5}\)
87
87 lượt xem
Xem đáp án
2 năm trước
Câu 2:

Nhị thức \(f\left( x \right) = 3x + 2\) nhận giá trị âm khi: 

\(x < \dfrac{3}{2}\).    
\(x <  - \dfrac{2}{3}\). 
\(x > \dfrac{3}{2}\).
\(x >  - \dfrac{2}{3}\).
88
88 lượt xem
Xem đáp án
2 năm trước
Câu 3:

Cho hàm số \(y = ax + b\), trong đó a,b là tham số, \(a > 0\). Mệnh đề nào sau đây đúng ?

Hàm số \(y = ax + b\) nhận giá trị dương trên \(\mathbb{R}\)                   
Hàm số \(y = ax + b\) nhận giá trị âm trên \(\left( { - \dfrac{b}{a}; + \infty } \right)\)      
Hàm số \(y = ax + b\) nhận giá trị âm trên \(\mathbb{R}\)      
Hàm số \(y = ax + b\) nhận giá trị dương trên \(\left( { - \dfrac{b}{a}; + \infty } \right)\)
82
82 lượt xem
Xem đáp án
2 năm trước
Câu 4:

Tập nghiệm của bất phương trình \(\dfrac{2}{x} >  - 1\) là:

\(\left( { - 2;0} \right)\)
\(\left( { - \infty ; - 2} \right)\)
\(\left( { - \infty ; - 2} \right) \cup \left( {0; + \infty } \right)\)
\(\left( { - 2; + \infty } \right)\)
79
79 lượt xem
Xem đáp án
2 năm trước
Câu 5:

Cho biểu thức \(f\left( x \right) = x\left( {x - 2} \right)\left( {3 - x} \right).\) Tập hợp tất cả các giá trị của \(x\) thỏa mãn bất phương trình \(f\left( x \right) < 0\) là

\(x \in \left( {0;2} \right) \cup \left( {3; + \infty } \right).\)

\(x \in \left( { - \infty ;0} \right) \cup \left( {3; + \infty } \right).\)

\(x \in \left( { - \infty ;0} \right] \cup \left( {2; + \infty } \right).\)

\(x \in \left( { - \infty ;0} \right) \cup \left( {2;3} \right).\)
94
94 lượt xem
Xem đáp án
2 năm trước
Câu 6:

Cho biểu thức \(f\left( x \right) = 9{x^2} - 1.\) Tập hợp tất cả các giá trị của \(x\) để \(f\left( x \right) < 0\) là

 

\(x \in \left[ { - \dfrac{1}{3};\dfrac{1}{3}} \right].\)

\(x \in \left( { - \infty ; - \dfrac{1}{3}} \right) \cup \left( {\dfrac{1}{3}; + \infty } \right).\)

\(x \in \left( { - \infty ; - \dfrac{1}{3}} \right] \cup \left[ {\dfrac{1}{3}; + \infty } \right).\)

\(x \in \left( { - \dfrac{1}{3};\dfrac{1}{3}} \right).\)
144
144 lượt xem
Xem đáp án
2 năm trước
Câu 7:

Cho biểu thức \(f\left( x \right) = \left( {2x - 1} \right)\left( {{x^3} - 1} \right).\) Tập hợp tất cả các giá trị của \(x\) thỏa mãn bất phương trình \(f\left( x \right) \ge 0\) là

\(x \in \left[ {\dfrac{1}{2};1} \right].\)

\(x \in \left( { - \infty ; - \dfrac{1}{2}} \right) \cup \left( {1; + \infty } \right).\)

\(x \in \left( { - \infty ;\dfrac{1}{2}} \right] \cup \left[ {1; + \infty } \right).\)

\(x \in \left( {\dfrac{1}{2};1} \right).\)
133
133 lượt xem
Xem đáp án
2 năm trước

Đề thi - đề kiểm tra Xem thêm
icon Hỏi bài tập
Hỏi bài tập Xem thêm
Học lý thuyết MÔN TOÁN Lớp 10 vững kiến thức đứng top 1 lớp