Câu nào sau đây không đúng khi nói về thấu kính hội tụ
A, B, D - đúng
C - sai vì thấu kính hội tụ được làm bằng các vật liệu trong suốt như nhựa, ...
Cho một thấu kính có tiêu cự là 20cm. Độ dài FF’ giữa hai tiêu điểm của thấu kính là:
Ta có: \(OF = OF' = f\) - tiêu cự của thấu kính
Ta suy ra: \(FF' = 2f = 2.20 = 40cm\)
Cho một thấu kính hội tụ có khoảng cách giữa hai tiêu điểm là $60cm$. Tiêu cự của thấu kính là:
Ta có: \(OF = OF' = f\) - tiêu cự của thấu kính
\(\begin{array}{l}FF' = 2f = 60cm\\ \to f = \dfrac{{60}}{2} = 30cm\end{array}\)
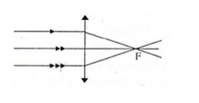
Dùng một thấu kính hội tụ hứng ánh sáng Mặt Trời theo phương song song với trục chính của thấu kính thì:
Ta có: Một chùm tia tới song song với trục chính của thấu kính hội tụ cho chùm tia ló hội tụ tại tiêu điểm của thấu kính.
Đặt vật sáng nhỏ vuông góc với trục chính của một thấu kính hội tụ và cách thấu kính 20 cm. Biết tiêu cự thấu kính bằng 15 cm. Ảnh của vật sáng cho bởi thấu kính là
Ta có: \(\left\{ \begin{array}{l}d = 20cm\\f = 15m \Rightarrow 2f = 30cm\end{array} \right. \Rightarrow d < f < 2f\)
→ Ảnh của vật sáng cho bởi thấu kính là ảnh thật, lớn hơn vật.
Một vật sáng AB có dạng mũi tên được đặt vuông góc với trục chính của một thấu kính hội tụ có tiêu cự f = 12cm. Điểm A nằm trên chục chính cách thấu kính 16cm. Ảnh A'B' của AB qua thấu kính cách kính một khoảng bao nhiêu
Ta có: \(\dfrac{1}{f} = \dfrac{1}{d} + \dfrac{1}{{d'}} \Rightarrow d' = \dfrac{{f.d}}{{d - f}} = \dfrac{{12.16}}{{16 - 12}} = 48cm\)
Đặt vật AB trước thấu kính hội tụ có tiêu cự 10 cm. Muốn thu được ảnh thật nhỏ hơn vật phải đặt vật cách thấu kính bao nhiêu?
Thấu kính hội tụ tạo ra ảnh thật nhỏ hơn vật khi khoảng cách từ vật đến kính thoả mãn điều kiện :
\(d > 2f \Leftrightarrow d > 2.10 = 20 \Leftrightarrow d > 20cm\)
Một thấu kính hội tụ có tiêu cự f = 20cm. Vật AB cách thấu kính 40cm. Ảnh thu được là:
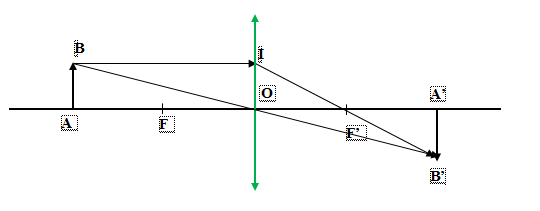
Ảnh thu được là ảnh thật, ngược chiều với vật.
Ta có: \(\Delta OAB \sim \Delta OA'B' \Rightarrow \frac{{AB}}{{A'B'}} = \frac{{OA}}{{OA'}} = \frac{{OA}}{{2f}}\,\,\left( 1 \right)\)
Ta có: \(\Delta OF'I \sim \Delta A'F'B' \Rightarrow \frac{{OI}}{{A'B'}} = \frac{{OF'}}{{A'F'}} \Leftrightarrow \frac{{AB}}{{A'B'}} = \frac{f}{{OA' - f}}\,\,\left( 2 \right)\)
Từ (1) và (2)
\(\begin{array}{l} \Rightarrow \frac{{2f}}{{OA'}} = \frac{f}{{OA' - f}}\, \Leftrightarrow \,\frac{{40}}{{OA'}} = \frac{{20}}{{OA' - 20}} \Rightarrow OA' = 40cm\\\left( 1 \right) \Rightarrow \frac{{A'B'}}{{AB}} = \frac{{2f}}{{OA'}} = 1 \Rightarrow A'B' = AB\end{array}\)
Vậy ảnh thu được là ảnh thật, cách thấu kính 40cm, ngược chiều vật và độ cao bằng vật

