Dùng máy ảnh để chụp ảnh một vật vuông góc với trục chính của vật kính. Gọi khoảng cách từ vật đến vật kính và từ vật kính đến phim lần lượt là \(4,5m\) và \(9cm\), độ cao của vật và ảnh lần lượt là \(h\) và \(h'\). Hệ thức nào sau đây là đúng?
Ta có: \(\left\{ \begin{array}{l}d = 4,5m\\d' = 9cm = 0,09m\end{array} \right.\)
Lại có:
\(\dfrac{h}{{h'}} = \dfrac{d}{{d'}} = \dfrac{{4,5}}{{0,09}} = 50 \to h = 50h'\)
Khi chụp ảnh một vật cao 1 m đặt cách máy ảnh 2 m. Ảnh của vật trên phim có độ cao 2,5 cm thì khoảng cách từ vật kính đến phim là:
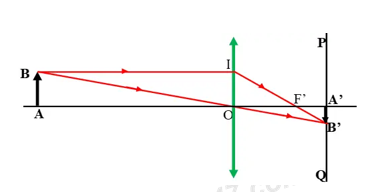
Ta có:
\(\begin{array}{l}
\Delta OAB \sim \Delta OA'B' \Rightarrow \frac{{OA'}}{{OA}} = \frac{{A'B'}}{{AB}} \Leftrightarrow \frac{{OA'}}{2} = \frac{{2,5}}{{100}}\\
\Rightarrow OA' = 0,05m = 5cm
\end{array}\)
Vậy khoảng cách từ vật kính đến phim là 5 cm.
Một vật AB đặt trước một máy ảnh và cách vật kính của máy 3,6m. Ta thu được một ảnh trên phim cao 2,5cm và cách vật kính 12 cm. Chiều cao của vật AB là:
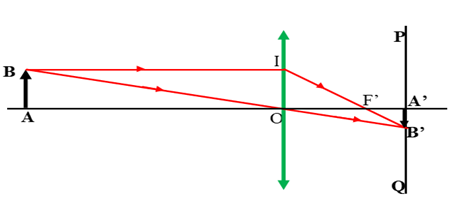
OA = 3,6m = 360cm; A’B’ = 2,5cm; OA’ = 12cm; AB = ?
Ta có \(\Delta OA'B' \sim \Delta OAB \Rightarrow \dfrac{{A'B'}}{{AB}} = \dfrac{{OA'}}{{OA}} \Rightarrow AB = \dfrac{{A'B'.OA}}{{OA'}} = \dfrac{{2,5.360}}{{12}} = 75cm = 0,75m\)
Một vật có dạng một đoạn thẳng, đặt vuông góc với trục chính của vật kính (hình vẽ). Trong hình này: AB là vật, O là quang tâm của vật kính, PQ là vị trí đặt màn hứng ảnh, khoảng cách từ vật đến vật kính là 2m, từ màn hứng ảnh đến vật kính là 5cm. Hình vẽ không cần đúng tỉ lệ. Tính tỉ số giữa chiều cao của ảnh với chiều cao của vật.
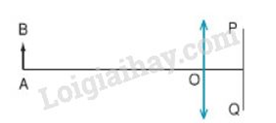
Vẽ ảnh của vật AB:
– Từ B kẻ tia tới qua quang tâm O thì tia ló truyền thẳng tới cắt phim PQ tại ảnh B' của B.
– Từ B kẻ tia tới BI song song với trục chính cho tia ló IB’. Tia ló này cắt trục chính tại tiêu điểm F'.
– Hạ B’ vuông góc với trục chính thì A’B’ là ảnh của AB tạo bởi vật kính.
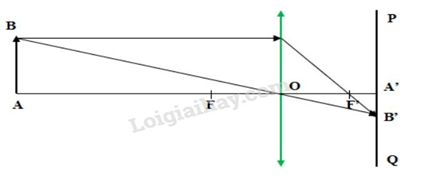
OA = 2m = 200cm; OA’ = 5cm
Ta có: \(\Delta OA'B' \sim \Delta OAB \Rightarrow \dfrac{{A'B'}}{{AB}} = \dfrac{{OA'}}{{OA}} = \dfrac{5}{{200}} = \dfrac{1}{{40}}\)
