Ảnh của một vật sáng đặt ngoài khoảng tiêu cự của thấu kính hội tụ có tiêu cự \(f = 16cm\). Có thể thu được ảnh nhỏ hơn vật tạo bởi thấu kính này khi đặt vật cách thấu kính:
Ta có: Để thu được ảnh thật ngược chiều, nhỏ hơn vật => vật phải cách thấu kính một khoảng \(d > 2f\)
Theo đầu bài ta có: \(f = 16cm \to 2f = 32cm\)
=> Để thu được ảnh nhỏ hơn vật => vật cần đặt cách thấu kính một khoảng \(d > 32cm\)
Một thấu kính hội tụ có tiêu cự \(f = 20cm\). Một vật thật AB cách thấu kính \(40cm\). Ảnh thu được là:
Ta có, \(f = 20cm;d = 40cm\)
+ Vật đặt tại \(d = 2f = 40cm\) => ảnh thu được là ảnh thật ngược chiều với vật và bằng vật
+ Áp dụng biểu thức: \(\dfrac{1}{f} = \dfrac{1}{d} + \dfrac{1}{{d'}}\)
Ta suy ra: \(d' = \dfrac{{f.d}}{{d - f}} = \dfrac{{20.40}}{{40 - 20}} = 40cm\)
=> Ảnh thu được là ảnh thật ngược chiều với vật, cách thấu kính một khoảng 40cm và cao bằng vật.
Một vật đặt vuông góc với trục chính của một thấu kính hội tụ, cho ảnh ảo cao gấp 3 lần vật. Ảnh cách vật 32cm. Tiêu cự của thấu kính là bao nhiêu?
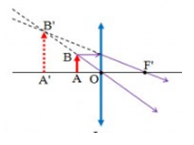
+ ảnh ảo cao gấp 3 lần vật, ta suy ra: \(\frac{h}{{h'}} = \frac{1}{3} = \frac{d}{{d'}} \to d' = 3{\rm{d}}\)
+ Lại có: d' - d =32 => 3d - d = 32 => d = 16 (cm)
+ Do ảnh là ảnh ảo, sử dụng công thức thấu kính, ta có:
\(\begin{array}{l}\frac{1}{f} = \frac{1}{d} - \frac{1}{{d'}}\\ \to f = \frac{{d'.d}}{{d' - d}} = \frac{{3{\rm{d}}.d}}{{3{\rm{d}} - d}} = \frac{3}{2}d = \frac{3}{2}.16 = 24cm\end{array}\)

