Kết quả:
0/40
Thời gian làm bài: 00:00:00
Một chất điểm dao động điều hòa có phương trình vận tốc \(v = 2\pi cos\left( {2\pi t + \dfrac{\pi }{6}} \right)cm/s\). Lấy \({\pi ^2} = 10\). Biểu thức gia tốc tức thời của chất điểm là:
Một con lắc đơn gồm vật nặng có khối lượng \(m\), dây treo dài \(l\). Kéo vật ra khỏi vị trí cân bằng một góc \({\alpha _0}\) rồi thả cho vật dao động. Biểu thức xác định lực căng dây tại vị trí \(\alpha \) bất kì là:
Tại một nơi xác định, chu kì dao động điều hòa của con lắc đơn tỉ lệ thuận với:
Khi xảy ra hiện tượng cộng hưởng cơ thì vật tiếp tục dao động:
Một khung dây dẫn có diện tích $S = 50 cm^2$ gồm $150$ vòng dây quay đều với vận tốc n vòng/phút trong một từ trường đều \(\vec B\) vuông góc trục quay \(\Delta \) và có độ lớn $B = 0,02 T$. Từ thông cực đại gửi qua khung là:
Chọn câu trả lời sai. Năng lượng của sóng truyền từ một nguồn điểm sẽ:
Trong mạch R, L, C nối tiếp với điện áp hai đầu đoạn mạch là u và cường độ dòng điện qua mạch là i. Chọn phát biểu đúng:
Trong dao động điều hòa, vì cơ năng được bảo toàn nên
Khi có sóng dừng trên một sợi dây đàn hồi, khoảng cách từ một bụng đến nút gần nó nhất bằng:
Chọn phát biểu sai về quan hệ giữa chuyển động tròn đều và dao động điều hoà là hình chiếu của nó.
Con lắc lò xo treo thẳng đứng có độ cứng k, khối lượng m, \(\Delta l\) là độ dãn của lò xo khi ở vị trí cân bằng, g là gia tốc trọng trường. Tần số của con lắc được xác định bởi biểu thức:
Chọn phát biểu đúng khi sóng cơ truyền càng xa nguồn thì:
Trong dao động điều hoà
Mạch điện xoay chiều nào sau đây có hệ số công suất nhỏ nhất. Với R là điện trở thuần, L là độ tự cảm, C là điện dung:
Nhận xét nào sau đây là sai khi nói về sóng âm
Cho L là độ tự cảm, f là tần số, T là chu kì, \(\omega \) là tần số góc. Biểu thức tính cảm kháng của cuộn cảm là:
Giảm xóc của ô tô là áp dụng của
Thế nào là 2 sóng kết hợp?
Một vật dao động điều hòa có biên độ là \(2{\rm{ }}\left( {cm} \right)\) và tần số góc \(\omega = 2\pi \left( {rad} \right)\) . Lấy \({\pi ^2} = 10\), gia tốc của vật tại thời điểm vật có vận tốc \(v = 2\sqrt 3 \pi cm/s\) là:
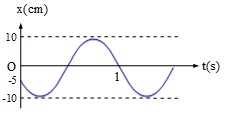
Một chất điểm dao động điều hòa có đồ thị biểu diễn sự phụ thuộc vào thời gian của li độ như hình vẽ. Phương trình dao động của vật là:
Vật dao động điều hoà theo phương trình $x = 5\cos \left( {2\pi t - \frac{\pi }{4}} \right)cm$. Tốc độ trung bình của vật đi được trong khoảng thời gian từ ${t_1} = 1s$ đến ${t_2} = 4,625s$ là:
Một vật dao động điều hòa với phương trình $x=10cos(4\pi t)cm$ . Tại thời điểm mà động năng bằng $3$ lần thế năng thì vật ở cách VTCB một khoảng:
Một con lắc đơn dao động với biên độ góc α0 = 0,1 rad có chu kì dao động T = 1s. Chọn gốc tọa độ là vị trí cân bằng, khi vật bắt đầu chuyển động vật đi qua vị trí cân bằng theo chiều âm. Phương trình dao động của con lắc là:
Con lắc đơn có khối lượng \(200g\) dao động với phương trình \(s = 10sin(2t) cm\). Ở thời điểm \(t = \dfrac{\pi }{6}s\), con lắc có động năng là:
Dao động tổng hợp của hai dao động điều hòa cùng phương , cùng tần số có phương trình li độ là x = 3cos(πt - 5π/6) (cm). Biết dao động thứ nhất có phương trình li độ là x1 = 5cos(πt + π/6) (cm). Dao động thứ hai có phương trình li độ là:
Một nguồn phát sóng dao động theo phương trình \(u = ac{\rm{os4}}\pi {\rm{t}}\) (cm). Trong khoảng thời gian 2s sóng truyền đi được quãng đường bằng bao nhiêu lần bước sóng?
Một sợi dây đàn hồi nằm ngang có điểm đầu O dao động theo phương đứng với biên độ \(3cm\), chu kì truyền sóng 0,5s. Vận tốc truyền sóng là \(32cm/s\). Sóng truyền từ O đến M. Viết phương trình sóng tại M cách O \(d{\rm{ }} = {\rm{ }}50{\rm{ }}cm\).
Hai nguồn sóng cơ $AB$ cách nhau dao động chạm nhẹ trên mặt chất lỏng, cùng tấn số $100Hz$, cùng pha theo phương vuông vuông góc với mặt chất lỏng. Vận tốc truyền sóng $20m/s$.Số điểm không dao động trên đoạn $AB = 1m$ là :
Một dây đàn hồi AB đầu A được rung nhờ một dụng cụ để tạo thành sóng dừng trên dây, biết phương trình dao động tại đầu A là \({u_A} = {\rm{ }}acos50\pi t\left( {cm} \right)\). Quan sát sóng dừng trên sợi dây ta thấy trên dây có những điểm không phải là điểm bụng dao động với biên độ b \((b \ne 0)\) cách đều nhau và cách nhau khoảng \(0,6m\). Giá trị của b và tốc truyền sóng trên sợi dây lần lượt là:
Dòng điện xoay chiều hình sin chạy qua một đoạn mạch có biểu thức cường độ là
$i = {I_0}{\text{cos}}\left( {\omega t - \dfrac{\pi }{2}} \right)A$ , I0>0. Tính từ lúc t=0(s), điện lượng chuyển qua tiết diện phẳng của dây dẫn của đoạn mạch đó trong thời gian bằng nửa chu kì của dòng điện là:
Một đoạn mạch nối tiếp gồm một cuộn dây và một tụ điện. Hiệu điện thế hiệu dụng hai đầu đoạn mạch, hai đầu cuộn dây, hai đầu tụ điện đều bằng nhau. Hệ số công suất \(cosφ\) của đoạn mạch là:
Đặt điện áp \(u = 200\cos 100\pi t\left( V \right)\) vào hai đầu đoạn mạch gồm điện trở \(100 Ω\), cuộn cảm thuần và tụ điện mắc nối tiếp. Biết trong đoạn mạch có cộng hưởng điện. Cường độ hiệu dụng của dòng điện trong đoạn mạch là
Mạch điện xoay chiều RLC nối tiếp. Hai đầu đoạn mạch có một điện áp xoay chiều có tần số và điện áp hiệu dụng không đổi. Dùng vôn kế có điện trở rất lớn, lần lượt đo điện áp ở hai đầu đoạn mạch, hai đầu tụ điện và hai đầu cuộn dây thì số chỉ của vôn kế tương ứng là \(U\), \({U_C}\) và \({U_L}\) . Biết \(U = \dfrac{{{U_C}}}{{\sqrt 2 }} = \sqrt 2 {U_L}\). Hệ số công suất của mạch là:
Cho mạch điện như hình. Điện áp \({u_{AB}} = 80\cos 100\pi t(V)\), \(r = 15Ω\), \(L = \dfrac{1}{{5\pi }}H\)
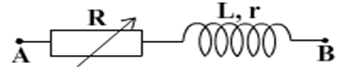
Điều chỉnh biến trở R để công suất tiêu thụ trên R cực đại. Tính R và PRmax.
Đặt điện áp \(100V - 25Hz\) vào hai đầu đoạn mạch mắc nối tiếp gồm cuộn dây có điện trở thuần \(r\), cuộn cảm có độ tự cảm \(L\) và tụ điện có điện dung \(C = \dfrac{{0,1}}{\pi }mF\). Biết điện áp hai đầu cuộn dây sớm pha hơn dòng điện trong mạch là \(\dfrac{\pi }{6}\), đồng thời điện áp hiệu dụng hai đầu cuộn dây gấp đôi trên tụ điện. Công suất tiêu thụ của toàn mạch là:
Điện năng tiêu thụ ở một trạm phát điện được truyền dưới điện áp hiệu dụng là $2kV$, công suất $200kW$. Hiệu số chỉ của công to điện nơi phát và nơi thu sau mỗi ngày đêm chênh lệch $480 kWh$. Hiệu suất của quá trinh tải điện là:
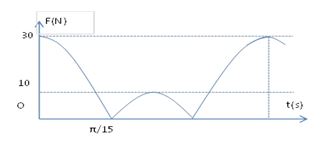
Một con lắc lò xo treo thẳng đứng tại nơi có \(g{\rm{ }} = 10m/{s^2}\) đang dao động điều hòa trên trục Ox thẳng đứng hướng lên. Cho đồ thị biểu diễn độ lớn của lực đàn hồi lò xo vào thời gian như hình vẽ. Độ cứng lò xo và khối lượng vật nặng lần lượt bằng
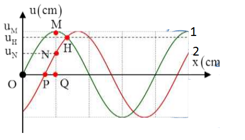
Một nguồn phát sóng cơ hình sin đặt tại O, truyền dọc theo sợi dây đàn hồi căng ngang rất dài OA với bước sóng \(24cm\). Tại thời điểm \({t_1}\) và \({t_2}\) hình dạng của một đoạn dây tương ứng như đường 1 và đường 2 của hình vẽ, trục Ox trùng với vị trí cân bằng của sợi dây, chiều dương trùng với chiều truyền sóng. Trong đó, M là điểm cao nhất, \({u_M},{\rm{ }}{u_N},{\rm{ }}{u_H}\) lần lượt là li độ của các điểm M, N, H. Biết \(u_M^2 = u_{N}^2 + u_H^2\) và biên độ sóng không đổi. Khoảng cách từ P đến Q bằng:
Đặt điện áp \(u = {U_0}{\rm{cos100}}\pi {\rm{t}}\left( V \right)\) (t tính bằng s) vào đoạn mạch gồm cuộn dây và tụ điện mắc nối tiếp. Cuộn dây có độ tự cảm \(L = \dfrac{{1,5}}{\pi }H\), điện trở \(r = 50\sqrt 3 \Omega \), tụ điện có điện dung \(C = \dfrac{{{{10}^{ - 4}}}}{\pi }F\) . Tại thời điểm t1, điện áp tức thời giữa hai đầu cuộn dây có giá trị $150V$, đến thời điểm \({t_1} + \dfrac{1}{{75}}s\) thì điện áp giữa hai đầu tụ điện cũng bằng $150V$. Giá trị của U0 bằng
Một vật có khối lượng không đổi, thực hiện đồng thời hai dao động điều hòa có phương trình dao động lần lượt là \({x_1} = 8cos\left( {2\pi t + \varphi } \right)cm\) và \({x_2} = {A_2}cos(2\pi t - \dfrac{\pi }{2})cm\) thì dao động tổng hợp là \(x = Acos(2\pi t - \dfrac{\pi }{6})cm\). Để biên độ dao động tổng hợp của vật đạt giá trị lớn nhất thì \({A_2}\) có giá trị là:

