Câu hỏi:
2 năm trước
Đặt điện áp \(100V - 25Hz\) vào hai đầu đoạn mạch mắc nối tiếp gồm cuộn dây có điện trở thuần \(r\), cuộn cảm có độ tự cảm \(L\) và tụ điện có điện dung \(C = \dfrac{{0,1}}{\pi }mF\). Biết điện áp hai đầu cuộn dây sớm pha hơn dòng điện trong mạch là \(\dfrac{\pi }{6}\), đồng thời điện áp hiệu dụng hai đầu cuộn dây gấp đôi trên tụ điện. Công suất tiêu thụ của toàn mạch là:
Trả lời bởi giáo viên
Đáp án đúng: b
Ta có:
+ Dung kháng của mạch: \({Z_C} = \dfrac{1}{{\omega C}} = \dfrac{1}{{2\pi fC}} = \dfrac{1}{{2\pi .25.\dfrac{{0,1}}{\pi }{{.10}^{ - 3}}}} = 200\Omega \)
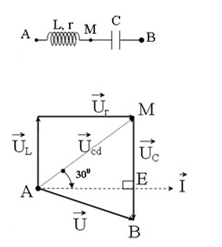
Từ giản đồ,
Xét \(\Delta AME\) , có:
\(\begin{array}{l}\sin \widehat {MAE} = \dfrac{{ME}}{{AM}} \Leftrightarrow \sin {30^0} = \dfrac{{ME}}{{AM}}\\ \Rightarrow ME = AM\sin {30^0} = \dfrac{{AM}}{2} = \dfrac{{{U_{cd}}}}{2}\end{array}\)
Mà theo đầu bài ta có, \({U_{cd}} = 2{U_C}\)
Ta suy ra: \(ME = {U_C}\) hay \(E \equiv M\)
\( \Rightarrow {U_L} = {U_C}\) => Mạch cộng hưởng \( \Rightarrow {U_R} = U = 100V\)
+ Ta có:
\(\begin{array}{l}\tan {30^0} = \dfrac{{{U_C}}}{{{U_R}}} \Rightarrow {U_C} = {U_R}\tan {30^0}\\ \Rightarrow {Z_C} = R.\tan {30^0}\\ \Rightarrow R = \dfrac{{{Z_C}}}{{\tan {{30}^0}}} = \dfrac{{200}}{{\dfrac{1}{{\sqrt 3 }}}} = 200\sqrt 3 \Omega \end{array}\)
+ Công suất của mạch khi đó: \(P = {P_{max}} = \dfrac{{{U^2}}}{R} = \dfrac{{{{100}^2}}}{{200\sqrt 3 }} = \dfrac{{50}}{{\sqrt 3 }}{\rm{W}}\)
Hướng dẫn giải:
+ Sử dụng biểu thức tính dung kháng: \({Z_C} = \dfrac{1}{{\omega C}} = \dfrac{1}{{2\pi fC}}\)
+ Sử dụng giản đồ véc-tơ và các hệ thức trong tam giác
+ Nhận biết bài toán cộng hưởng điện
