Câu hỏi:
2 năm trước
Một vật có khối lượng không đổi, thực hiện đồng thời hai dao động điều hòa có phương trình dao động lần lượt là \({x_1} = 8cos\left( {2\pi t + \varphi } \right)cm\) và \({x_2} = {A_2}cos(2\pi t - \dfrac{\pi }{2})cm\) thì dao động tổng hợp là \(x = Acos(2\pi t - \dfrac{\pi }{6})cm\). Để biên độ dao động tổng hợp của vật đạt giá trị lớn nhất thì \({A_2}\) có giá trị là:
Trả lời bởi giáo viên
Đáp án đúng: a
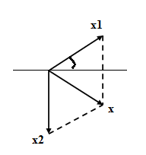
Áp dụng định lí hàm số sin, ta có:
\(\begin{array}{l}\dfrac{{{A_1}}}{{\sin {{60}^0}}} = \dfrac{{{A_2}}}{{\sin \left( {{{30}^0} + \varphi } \right)}} = \dfrac{A}{{\sin \left( {{{90}^0} - \varphi } \right)}}\\ \leftrightarrow \dfrac{8}{{\sin {{60}^0}}} = \dfrac{{{A_2}}}{{\sin \left( {{{30}^0} + \varphi } \right)}} = \dfrac{A}{{\sin \left( {{{90}^0} - \varphi } \right)}}\\ \to A = \dfrac{{8.\sin \left( {{{90}^0} - \varphi } \right)}}{{\sin {{30}^0}}}\end{array}\)
Để biên độ dao động tổng hợp của vật đạt giá trị lớn nhất khi \(\sin \left( {90 - \varphi } \right) = 1\)
\( \to \varphi = 0\)
Ta suy ra: \({A_2} = \dfrac{{8.\sin {{30}^0}}}{{\sin {{60}^0}}} = \dfrac{8}{{\sqrt 3 }}cm\)
Hướng dẫn giải:
+ Sử dụng giản đồ vectơ
+ Áp dụng định lí hàm số sin: \(\dfrac{a}{{\sin a}} = \dfrac{b}{{\sin b}} = \dfrac{c}{{\sin c}}\)
