Câu hỏi:
3 năm trước
Vật dao động điều hòa theo phương trình: \(x = 5c{\rm{os}}\left( {2\pi t - \frac{\pi }{3}} \right)cm\). Xác định thời gian ngắn nhất kể từ khi vật bắt đầu chuyển động đến vị trí có li độ \(x = \frac{{5\sqrt 2 }}{2}\) lần thứ nhất?
Trả lời bởi giáo viên
Đáp án đúng: c
Ta có:
Chu kỳ dao động của vật: $T = \frac{{2\pi }}{\omega } = \frac{{2\pi }}{{2\pi }} = 1{\rm{s}}$
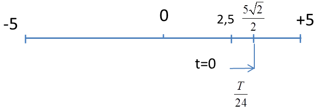
Tại thời điểm ban đầu t=0: $\left\{ \begin{array}{l}x = 5c{\rm{os}}\left( { - \frac{\pi }{3}} \right) = 2,5cm\\v = - 10\pi \sin \left( { - \frac{\pi }{3}} \right) = 5\sqrt 3 \pi > 0\end{array} \right.$
$ \to t = \frac{T}{{24}} = \frac{1}{{24}}s$
Hướng dẫn giải:
+ Sử dụng công thức xác định chu kỳ: $T = \frac{{2\pi }}{\omega }$
+ Sử dụng trục thời gian trên đường thẳng được suy ra từ đường tròn

